题目内容
如图甲所示，一个绝缘倾斜直轨道固定在竖直面内，轨道的AB部分粗糙，BF部分光滑．整个空间存在着竖直方向的周期性变化的匀强电场，电场强度随时间的变化规律如图乙所示，t=0时电场方向竖直向下．在虚线的右侧存在着垂直纸面向里的匀强磁场，磁感应强度为B=
．现有一个质量为m，电量为q的带正电的物体（可以视为质点），在t=0时从A点静止释放，物体与轨道间的动摩擦因数为μ，t=2s时刻，物体滑动到B点．在B点以后的运动过程中，物体没有离开磁场区域，物体在轨道上BC段的运动时间为1s，在轨道上CD段的运动时间也为1s．（物体所受到的洛伦兹力小于2mgcosθ）
（1）若轨道倾角为θ，求物块滑动到B的速度大小．
（2）若轨道倾角θ角未知，而已知BC及CD的长度分别为S1、S2，求出倾角θ的三角函表达式（用S1、S2、g表示）
（3）观察物体在D点以后的运动过程中，发现它并未沿着斜面运动，而且物块刚好水平打在H点处的竖直挡板（高度可以忽略）上停下，斜面倾角θ已知，求F点与H点的间距L．
| 2πm | q |
（1）若轨道倾角为θ，求物块滑动到B的速度大小．
（2）若轨道倾角θ角未知，而已知BC及CD的长度分别为S1、S2，求出倾角θ的三角函表达式（用S1、S2、g表示）
（3）观察物体在D点以后的运动过程中，发现它并未沿着斜面运动，而且物块刚好水平打在H点处的竖直挡板（高度可以忽略）上停下，斜面倾角θ已知，求F点与H点的间距L．
分析：（1）在0～1s内，电场力方向竖直向下，根据牛顿第二定律求出加速度，从而根据运动学公式求出末速度，在1～2s内，电场力方向竖直向上，大小等于重力，物体做匀速直线运动．
（2）根据牛顿第二定律求出物体在光滑斜面上运动的加速度，根据相等时间内的位移之差是一恒量，求出倾角θ的表达式．
（3）物体在D点重力和电场力平衡，做匀速圆周运动，圆弧的轨迹恰好相切于H点，根据几何关系，结合带电粒子在匀强磁场中的半径公式求出F点与H点的间距L．
（2）根据牛顿第二定律求出物体在光滑斜面上运动的加速度，根据相等时间内的位移之差是一恒量，求出倾角θ的表达式．
（3）物体在D点重力和电场力平衡，做匀速圆周运动，圆弧的轨迹恰好相切于H点，根据几何关系，结合带电粒子在匀强磁场中的半径公式求出F点与H点的间距L．
解答：
解：（1）由题意可知 qE=mg
t=0 到t=1s过程中，对物体有
2mgsinθ-2μmgcosθ=ma
t=1s到t=2s过程中物体做匀速直线运动，所以
VB=at0=2gsinθ-2μgcosθ
其中t0=1s
（2）物体在t=2s到t=3s做匀加速直线运动，加速度为
a'=2gsinθ
在t=3s到t=4s做匀速圆周运动，周期为T=
=1s
刚好完成一周，在t=4s到t=5s继续以a'做匀加速运动到D点，则
S2-S1=a't02
解得：sinθ=
（3）物体运动到D点时速度为
VD=VB+a'?2t0=6gsinθ-2μg cosθ
离开D点后做匀速圆周运动，半径为R，轨迹如图，则qBVD=
由几何关系可知
=tan
联立解得L=
(3sinθ-μcosθ)tan
答：（1）若轨道倾角为θ，求物块滑动到B的速度大小为2gsinθ-2μgcosθ．
（2）倾角θ的三角函表达式为sinθ=
（用S1、S2、g表示）；
（3）F点与H点的间距L为
(3sinθ-μcosθ)tan
．
解：（1）由题意可知 qE=mg t=0 到t=1s过程中，对物体有
2mgsinθ-2μmgcosθ=ma
t=1s到t=2s过程中物体做匀速直线运动，所以
VB=at0=2gsinθ-2μgcosθ
其中t0=1s
（2）物体在t=2s到t=3s做匀加速直线运动，加速度为
a'=2gsinθ
在t=3s到t=4s做匀速圆周运动，周期为T=
| 2πm |
| qB |
刚好完成一周，在t=4s到t=5s继续以a'做匀加速运动到D点，则
S2-S1=a't02
解得：sinθ=
| S2-S1 |
| 2g |
（3）物体运动到D点时速度为
VD=VB+a'?2t0=6gsinθ-2μg cosθ
离开D点后做匀速圆周运动，半径为R，轨迹如图，则qBVD=
m
| ||
| R |
由几何关系可知
| L |
| R |
| θ |
| 2 |
联立解得L=
| g |
| π |
| θ |
| 2 |
答：（1）若轨道倾角为θ，求物块滑动到B的速度大小为2gsinθ-2μgcosθ．
（2）倾角θ的三角函表达式为sinθ=
| S2-S1 |
| 2g |
（3）F点与H点的间距L为
| g |
| π |
| θ |
| 2 |
点评：解决本题的关键搞清物体在整个过程中的运动情况，根据物体的受力，判断物体的运动，物体经历了匀加速直线运动、匀速直线运动，以及匀加速直线运动和匀速圆周运动，过程较复杂，且与数学几何结合的比较紧密，对数学能力的要求较高．
练习册系列答案
阅读快车系列答案
相关题目
如图甲所示，一个绝缘倾斜直轨道固定在竖直面内，轨道的AB部分粗糙，BF部分光滑．整个空间存在着竖直方向的周期性变化的匀强电场，电场强度随时间的变化规律如图乙所示，t=0时电场方向竖直向下．在虚线的右侧存在着垂直纸面向里的匀强磁场，磁感应强度为B=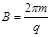
。现有一个质量为m，电量为q的带正电的物体（可以视为质点），在t=0时从A点静止释放，物体与轨道间的动摩擦因数为
。现有一个质量为m，电量为q的带正电的物体（可以视为质点），在t=0时从A点静止释放，物体与轨道间的动摩擦因数为
，t=2s时刻，物体滑动到B点。在B点以后的运动过程中，物体没有离开磁场区域，物体在轨道上BC段的运动时间为1s，在轨道上CD段的运动时间也为1s。（物体所受到的洛伦兹力小于2mgcosθ）
，求物块滑动到B的速度大小。
。现有一个质量为m，电量为q的带正电的物体（可以视为质点），在t=0时从A点静止释放，物体与轨道间的动摩擦因数为
，t=2s时刻，物体滑动到B点。在B点以后的运动过程中，物体没有离开磁场区域，物体在轨道上BC段的运动时间为1s，在轨道上CD段的运动时间也为1s。（物体所受到的洛伦兹力小于2mgcosθ）
，求物块滑动到B的速度大小。
