题目内容
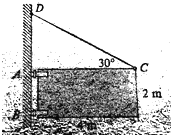 (2013?普陀区二模)一扇大门宽为4m,高为2m,质量为40kg,重心在门的中心,门在A、B处各用铰链相连.为减轻A处铰链的负担,将钢丝CD系在门上,CD与AC间夹角为30°,如图所示.增加CD上的张力,直到铰链A处的水平作用力为零,则在铰链B处作用力的水平分量为( )
(2013?普陀区二模)一扇大门宽为4m,高为2m,质量为40kg,重心在门的中心,门在A、B处各用铰链相连.为减轻A处铰链的负担,将钢丝CD系在门上,CD与AC间夹角为30°,如图所示.增加CD上的张力,直到铰链A处的水平作用力为零,则在铰链B处作用力的水平分量为( )分析:以D点为支点,根据力矩平衡条件:顺时针力矩之和等于逆时针力矩之和,列出求解.A、B两处竖直方向分力的力臂为零,力矩为零.
解答:解:设在铰链B处作用力的水平分量为F.
以D点为支点,铰链A、B两处竖直方向分力的力臂为零,力矩为零.
根据力矩平衡条件:
mg
AC=F(AB+ACtan30°)
得F=
=
N≈186N
故选D
以D点为支点,铰链A、B两处竖直方向分力的力臂为零,力矩为零.
根据力矩平衡条件:
mg
| 1 |
| 2 |
得F=
| mgAC |
| 2(AB+ACtan30°) |
| 400×4 |
| 2×(2+4tan30°) |
故选D
点评:本题的解题是选择支点,以D点为支点,铰链A、B两处竖直方向分力的力臂为零,力矩为零,比较简便.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
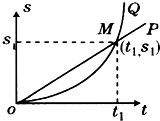 (2013?普陀区二模)如图所示为P、Q两物体沿同一直线作直线运动的s-t图,下列说法中正确的有( )
(2013?普陀区二模)如图所示为P、Q两物体沿同一直线作直线运动的s-t图,下列说法中正确的有( )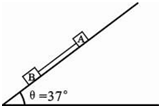 (2013?普陀区二模)如图所示,斜面与水平面间的夹角θ=37°,物体A和B的质量分别为mA=10kg、mB=5kg.A、B间用质量不计的细绳相连.试求:
(2013?普陀区二模)如图所示,斜面与水平面间的夹角θ=37°,物体A和B的质量分别为mA=10kg、mB=5kg.A、B间用质量不计的细绳相连.试求: