题目内容
（12分）如图所示，有一质量为M=2kg的平板小车静止在光滑的水平地面上，现有质量均为m=1kg的小物块A和B（均可视为质点），由车上P处分别以初速度v1=2m/s向左和v2=4m/s向右运动，最终A、B两物块恰好停在小车两端没有脱离小车。已知两物块与小车间的动摩擦因数都为μ=0.1，取g=10m/s2。求：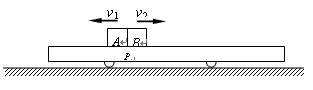
（1）小车的长度L；
（2）A在小车上滑动的过程中产生的热量；
（3）从A、B开始运动计时，经5s小车离原位置的距离。
（1）
（2）
（3）
解析试题分析：（1）由于开始时物块A、B给小车的摩擦力大小相等，方向相反，小车不动，物块A、B做减速运动，加速度a大小一样，但是A的初速度小，所以A的速度先减为零。
设A在小车上滑行的时间为t1，位移为s1，由牛顿定律
A做匀减速运动，由运动学公式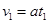
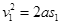
由以上三式可得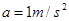 
，
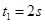
A在小车上滑动过程中，B也做匀减速运动，B的位移为s2，由运动学公式 
可得 
A在小车上停止滑动时，B的速度设为 v3，有
可得 
B继续在小车上减速滑动，而小车与A一起向右方向加速。因地面光滑，两个物块A、B和小车组成的系统动量守恒，设三者共同的速度为v，达到共速时B相对小车滑动的距离为
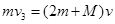
可得 
在此过程中系统损失的机械能为
可得 
故小车的车长
（2）由于A从开始滑动到相对小车静止以后，它随小车一起运动。故C点距小车左端的距离为
摩擦生热等于滑动摩擦力与相对位移的乘积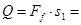 
（3）小车和A在摩擦力作用下一起做加速运动，由牛顿运动定律
可得小车运动的加速度 
小车加速运动的时间为
，小车匀速运动的时间为
可得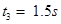 
所以 
经5s小车离原位置有
可得
考点：牛顿运动定律、动量定理、功能关系
，物块A恰能保持静止．现在物块B的下端再挂一个小物块Q，物块A可从图示位置上升并恰好能到达C处．不计摩擦和空气阻力，
、
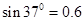，重力加速度g取10m/s2．求：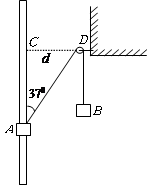
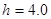m。一架质量为
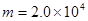kg的飞机，其喷气发动机的推力大小恒为
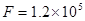N，方向与速度方向相同，在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍，假设航母处于静止状态，飞机质量视为不变并可看成质点，倾斜跑道看作斜面，不计拐角处的影响。取
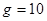m/s2。
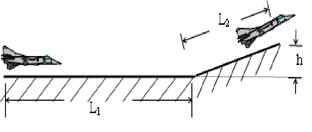
s2/m2，运动员和伞的总质量m=72kg．设跳伞塔足够高，且运动员跳离塔后即打开伞，取g=10m/s2．
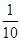，行星表面的重力加速度g是多大？
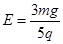。经过一段时间t，小球经过与A点在同一水平线上的B点。求