��Ŀ����
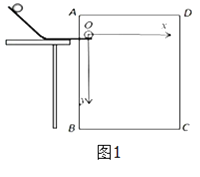
����Ŀ����ͼ��ʾ����ֱƽ�������ķ�֮һԲ������̶���ˮƽ�����ϣ�����¶���ˮƽ�������У�Բ��ΪO�㣬A���B��ֱ���Բ���������ߵ����͵㡣һС������Բ�����A�������ͷţ���B����ˮƽ����ɳ����䵽ˮƽ����C�㡣��֪Բ������⻬���뾶R=0.2 m��С���������m=1.0 kg��B�㵽ˮƽ����ĸ߶�h=0.8 m��ȡ�������ٶ�g=10 m/s2����
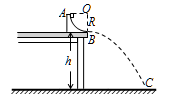
��1��С�����B��ɳ�ʱ���ٶ�vB����С��
��2����B�㣬Բ�������С����֧����FN�Ĵ�С��
��3��C����B���ˮƽ����x�Ĵ�С��
���𰸡���1��![]() m/s ��2��FN=30 N ��3��x=0.8 m
m/s ��2��FN=30 N ��3��x=0.8 m
����������1��С������Բ��������»������У��ɶ��ܶ�����![]()
��ã�![]() m/s
m/s
��2��С������B��ʱ����ţ�ٵڶ�����![]()
��ã�FN=30 N
��3��С�����B��ɳ�����ƽ���˶���![]()
��ã�![]() s
s
![]()
��ã�x=0.8 m

��ϰ��ϵ�д�
�����Ŀ