题目内容
【题目】如图，比荷分别为k和2k的甲、乙两带正电粒子
不计重力
，由静止状态经相同电压U加速后从坐标原点O沿x轴的正方向射入匀强磁场区域Ⅰ和匀强磁场区域Ⅱ，经两磁场后分别打在屏上
、
两点未标出。已知Ⅰ、Ⅱ两磁场是相邻的矩形区域，区域的宽均为a，区域的边界平行于y轴，两磁场的方向均与Oxy坐标平面垂直但方向相反，磁感应强度的大小均为
式中U为加速电压。屏垂直于x轴且到y轴的距离为6a。
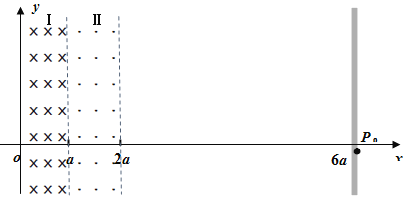
求甲、乙两粒子在磁场Ⅱ中运动的轨迹的半径之比
：
求与两点间的距离
若使甲、乙两粒子最终能打到屏上的同一点
见图且方向均沿x轴的正方向，可在磁场Ⅰ、Ⅱ的基础上再加上若干磁场区。
请在图中画出可能的磁场区域所在的位置并在图中标明磁场的方向
在的情况下，试求甲、乙两粒子从O点运动到
点的时间之比
：
。
【答案】（1）
； （2） 
；
（3）①
。
②
。
【解析】
由动能定理求得粒子速度，再根据洛伦兹力做向心力求得轨道半径；根据匀速圆周运动和匀速直线运动规律，由几何关系求得偏移，从而得到两点间的距离；根据速度方向变化得到磁场类型，在根据偏移量相等得到磁场宽度；根据几何关系得到粒子在磁场中转过的中心角，即可根据周期求得在磁场中的运动时间；再根据匀速直线运动规律得到在非磁场区域的运动时间，从而得到两粒子运动时间之比。
设粒子质量为m，电荷量为q，加速后的速度为v，那么，由动能定理可得：
，所以，
；
那么，粒子在磁场Ⅱ中运动的速度为v，粒子只受洛伦兹力作用，故粒子做匀速圆周运动，洛伦兹力做向心力，设轨道半径为R，则有：
；
所以，轨道半径
；故
，
那么，甲、乙两粒子在磁场Ⅱ中运动的轨迹的半径之比
；
由根据粒子的轨道半径，根据粒子在磁场中做匀速圆周运动，离开磁场后做匀速直线运动；
由几何关系可得：粒子在区域Ⅰ做逆时针旋转，在区域Ⅱ做顺时针旋转，且转动角度相同，故粒子离开磁场时的速度方向沿
方向；
故粒子打在屏上的纵坐标
；
故
，
，所以，
；
由可得：增加两个方向相反的磁场，磁场宽度相同且都小于轨道半径时，粒子离开磁场后的方向沿方向；
又有两粒子轨道半径不同，那么，每次偏转位移不等，故要使粒子打在同一位置，那么，后添加的磁场正好把前面磁场产生的偏转位移抵消；
根据几何关系可得：要使甲、乙两粒子最终能打到屏上的同一点且方向均沿x轴的正方向，只能在x轴
区间任意位置加上对称磁场，且沿方向，先向外后向里；
故可能的磁场区域如图所示：
甲粒子在每个磁场区间转过的中心角
，故在磁场中的运动时间
；
甲粒子在非磁场区间运动时间
；
乙粒子在每个磁场区间转过的中心角
，故在磁场中的运动时间
；
乙粒子在非磁场区间运动时间
；
故甲、乙两粒子从O点运动到
点的时间之比
；
