题目内容
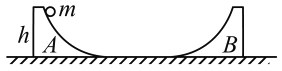
【题目】如图所示，形状完全相同的光滑弧形槽A, B静止在足够长的光滑水平面上，两弧形槽相对放置，底端与光滑水平面相切，弧形槽高度为h, A槽质量为2m, B槽质量为M。质量为m的小球，从弧形槽A顶端由静止释放，重力加速度为g，求:
(1)小球从弧形槽A滑下的最大速度;
(2)若小球从B上滑下后还能追上A，求M, m间所满足的关系:
【答案】（1）
（2）M＞3m
【解析】
（1）小球到达弧形槽A底端时速度最大。设小球到达弧形槽A底端时速度大小为v1，槽A的速度大小为v2。
小球与弧形槽A组成的系统在水平方向动量守恒，以水平向右为正方向，小球下滑过程中，由动量守恒定律得：mv1﹣2mv2＝0
由机械能守恒定律的：mgh＝
mv12+2mv22
联立解得：
，
（2）小球冲上弧形槽B后，上滑到最高点后再返回分离，设分离时小球速度反向，大小为v3，弧形槽B的速度为v4．整个过程二者水平方向动量守恒，则有：mv1＝﹣mv3+Mv4
二者的机械能守恒，则有：mv12＝mv32+Mv42
小球还能追上A，须有: v3＞v2。
解得: M＞3m
练习册系列答案
相关题目
