题目内容
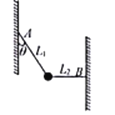
【题目】如图所示，A为内表面光滑的薄壁金属盒，其质量mA=0.5kg，底面长L=2.0m。A的中央位置放有可视为质点、质量mB=1.0kg的小球B．在A左侧与A相距s=0.61m处有一可视为质点、质量为mc=0.5kg的物块C，开始以v0=6.2m/s的速度向右沿直线运动，与A碰撞后粘在一起。已知A、C与水平面间的动摩擦因数均为μ=0.2，不考虑各物体相互碰撞的时间及B与A碰撞时的机械能损失，三物体始终在一条直线上运动，取g=10m/s2．求：
（1）C与A碰撞时速度的大小；
（2）从C与A结为一体到最后三物体都静止所经历的时间。
【答案】（1）6m/s（2）2.75s
【解析】试题分析：C与A碰撞前的速度大小为v1，由动能定理即可求出C与A碰撞时速度的大小；
C与A碰撞后粘在一起的速度为v2，由动量守恒定律求出共同速度，再根据动量定理和动能定理即可求出从C与A结为一体到最后三物体都静止所经历的时间。
（1）设C与A碰撞前的速度大小为v1，由动能定理：
解得：v1=6m/s
(2)设C与A碰撞后粘在一起的速度为v2，由动量守恒定律：
解得：v2=3m/s
A在运动
过程中，小球B保持静止，该过程时间为t1，设A与B碰撞前的速度为v3，
由动能定可得：
解得：v3=lm/s，t1=0.5s
设A第一次与与B碰撞后A和B的速度分别为v4和v5由动量守恒定律和机械能守恒定律：
解得：v4=0 v5=1m/s
B运动过程中盒子保持静止，设经过时间t2，B第二次与A碰撞：
第二次碰撞后A与B的速度分别为v6和v7，由动量守恒定律和机械能守恒定律
解得：v6=1m/s v7=0
A运动中B保持静止，设A滑动距离为x、时间为t3，由动能定理和动量定理
解得：x=0.125m<L、t3=0.25s
之后A与B均保持静止，从C开始运动到最后静止所经历的时间
