题目内容
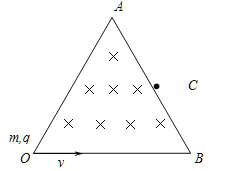
【题目】边长为L的等边三角形OAB区域内有垂直纸面向里的匀强磁场。在纸面内从O点向磁场区域AOB各个方向瞬时射入质量为m、电荷量为q的带正电的粒子,所有粒子的速率均为v 。如图所示,沿OB方向射入的粒子从AB边的中点C射出,不计粒子之间的相互作用和重力的影响,已知sin35°≈0.577。求:
(1)匀强磁场的磁感应强度;
(2)带电粒子在磁场中运动的最长时间;
(3)沿OB方向射入的粒子从AB边的中点C射出时,还在磁场中运动的粒子占所有粒子的比例。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)OC=Lcos30o=![]() L ①
L ①
沿OB方向射入的粒子从AB边的中点C射出,由几何知识得粒子做圆周运动的圆弧对的圆心角为60°。
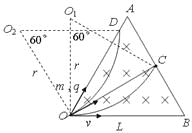
半径r= OC=![]() L ②
L ②
由qvB=![]() ③
③
得B=![]() =
=![]() ④
④
(2)从A点射出的粒子在磁场中运动时间最长 ⑤
设弦OA对的圆心角为![]() ,由几何关系得
,由几何关系得
sin![]() =
=![]() =
=![]() ≈0.577,
≈0.577, ![]() ≈70° ⑥
≈70° ⑥
最长时间tm≈![]() ⑦
⑦
(3)从OA上D点射出的粒子做圆周运动的弦长OD=OC,粒子做圆周运动的圆弧对的圆心角也为60°,如图,由几何知识得入射速度与OD的夹角应为30o ,即沿OC方向射入的粒子在磁场中运动的时间与沿OB方向射入的粒子从AB边的中点C射出的时间相等,从OB方向到OC方向这30o 范围内的粒子此时都还在磁场中,而入射的范围为60°,故还在磁场中运动的粒子占所有粒子的比例是![]() ⑧
⑧

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目