题目内容
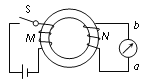
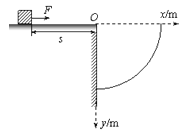
【题目】如图所示的平行板之间,存在着相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.20 T,方向垂直纸面向里,电场强度E1=1.0×105 V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有一边界线AO,与y轴的夹角∠AOy=45°,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度B2大小未知,边界线的下方有水平向右的匀强电场,电场强度E2=5.0×104 V/m,在x轴上固定一水平的荧光屏.一束带电荷量q=8.0×10-19C、质量m=8.0×10-26 kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为[0m,![]() ]的Q点垂直y轴射入磁场区,不计离子的重力,假设离子射出磁场后不再返回磁场。求:
]的Q点垂直y轴射入磁场区,不计离子的重力,假设离子射出磁场后不再返回磁场。求:

(1)离子在平行板间运动的速度大小.
(2)要使离子都不能打到x轴上,磁感应强度大小B2应满足什么条件?
(3)若![]() ,最后离子打到水平的荧光屏上的位置C,求离子打到荧光屏上的位置C时的动能.
,最后离子打到水平的荧光屏上的位置C,求离子打到荧光屏上的位置C时的动能.
【答案】(1) v=5.0×105 m/s (2) B2≥0.05 T (3) Ek=6.83×10-14J
【解析】
(1)设离子的速度大小为v,由于沿中线PQ做直线运动,则有qE1=qvB1,
代入数据解得v=5.0×105 m/s
(2)如图乙所示,

由几何关系可知使离子不能打到x轴上的最大半径 r,
![]()
解得:r=1m
设使离子都不能打到x轴上,最小的磁感应强度大小为B0,则![]()
代入数据解得B0=0.05 T,则B2≥0.05 T.
(3)离子进入磁场,做匀速圆周运动,由牛顿第二定律有![]()
![]()
作出离子的运动轨迹,设圆心为O′,运动轨迹交OA边界于N,如图甲所示》
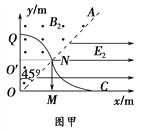
OQ=2r, 则OO′= r= O′N,∠N O′O=90°,过N点做速度方向,此方向竖直向下,离子垂直电场线进入电场,做类平抛运动,
y=OO′=r=vt ①
![]() ②
②
![]() ③
③
![]() ④
④
离子打到荧光屏上的位置C的动能为![]() ⑤
⑤
由①②③④⑤式解得:Ek=6.83×10-14J

 名校课堂系列答案
名校课堂系列答案