题目内容
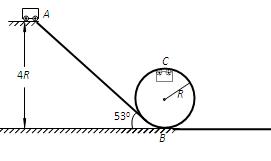
如图所示是一个设计“过山车”的试验装置的原理示意图,斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R.一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,A点距水平面的高度为4R,当它第一次经过B点进入圆形轨道时对轨道的压力为其重力的7倍,小车恰能完成圆周运动并第二次经过最低点B后沿水平轨道向右运动.已知重力加速度为g,斜面轨道与底面的夹角为530.(sin53°=0.8 cos53°=0.6)求:
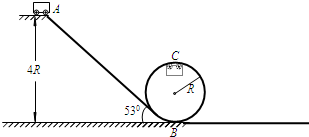
(1)小车第一次经过B点时的速度大小vB;
(2)小车在斜面轨道上所受阻力与其重力之比k;
(3)假设小车在竖直圆轨道左、右半圆轨道部分克服阻力做的功相等,求小车第二次经过竖直圆轨道最低点时的速度大小v′?

(1)小车第一次经过B点时的速度大小vB;
(2)小车在斜面轨道上所受阻力与其重力之比k;
(3)假设小车在竖直圆轨道左、右半圆轨道部分克服阻力做的功相等,求小车第二次经过竖直圆轨道最低点时的速度大小v′?
分析:(1)小车第一次经过B点时,由重力和轨道的支持力的合力提供向心力,根据牛顿第二定律求解速度vB.
(2)小车从A点到B点的过程,重力做功mg?4R.斜面长为L=
=5R,阻力做功-kmg?5R,初动能为零,末动能为
m
,根据动能定理求解k.
(3)小车在右半圆轨道上向上运动过程中,重力做功-2mgR,阻力做功-Wf.小车在左半圆轨道上向上运动过程中,重力做功2mgR,阻力做功-Wf.分别运用动能定理对两个运动过程进行研究,列方程,求出v′.
(2)小车从A点到B点的过程,重力做功mg?4R.斜面长为L=
| 4R |
| sin53° |
| 1 |
| 2 |
| v | 2 B |
(3)小车在右半圆轨道上向上运动过程中,重力做功-2mgR,阻力做功-Wf.小车在左半圆轨道上向上运动过程中,重力做功2mgR,阻力做功-Wf.分别运用动能定理对两个运动过程进行研究,列方程,求出v′.
解答:解:(1)设第一次小车运动到B点的速度大小为vB,受到的支持力为N,根据牛顿第二定律得
N-mg=m
解得 vB=
(2)小车从A点到B点的过程,根据动能定理有
mg?4R-kmg?5R=
m
解得k=0.2
(3)设小车在圆轨道最高点的速度为vC,由重力提供向心力,则有mg=m
解得vc=
设小车在右半圆轨道上克服阻力做功Wf,对小车从B点运动到C的点过程,根据动能定理有
-mg2R-Wf=
m
-
m
解得 Wf=
mgR
设小车第二次经过B点时的速度为v′,对小车从B点运动到C点再回到B点的过程,根据动能定理有:
-2Wf=
mv′2-
m
解得v′=2
答:
(1)小车第一次经过B点时的速度大小vB=
;
(2)小车在斜面轨道上所受阻力与其重力之比k=0.2;
(3)假设小车在竖直圆轨道左、右半圆轨道部分克服阻力做的功相等,小车第二次经过竖直圆轨道最低点时的速度大小v′=2
.
N-mg=m
| ||
| R |
解得 vB=
| 6gR |
(2)小车从A点到B点的过程,根据动能定理有
mg?4R-kmg?5R=
| 1 |
| 2 |
| v | 2 B |
解得k=0.2
(3)设小车在圆轨道最高点的速度为vC,由重力提供向心力,则有mg=m
| ||
| R |
解得vc=
| gR |
设小车在右半圆轨道上克服阻力做功Wf,对小车从B点运动到C的点过程,根据动能定理有
-mg2R-Wf=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
解得 Wf=
| 1 |
| 2 |
设小车第二次经过B点时的速度为v′,对小车从B点运动到C点再回到B点的过程,根据动能定理有:
-2Wf=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 B |
解得v′=2
| gR |
答:
(1)小车第一次经过B点时的速度大小vB=
| 6gR |
(2)小车在斜面轨道上所受阻力与其重力之比k=0.2;
(3)假设小车在竖直圆轨道左、右半圆轨道部分克服阻力做的功相等,小车第二次经过竖直圆轨道最低点时的速度大小v′=2
| gR |
点评:涉及力在空间的效应,要优先考虑动能定理.对于圆周运动,涉及力的问题,往往根据向心力进行分析处理.难度适中.

练习册系列答案
相关题目
 (2009?南充模拟)如图所示是一个设计“过山车”的试验装置的原理示意图,光滑斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R.一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,当它第一次经过B点进入圆形轨道时对轨道的压力为其重力的7倍,小车恰能完成圆周运动并第二次经过最低点沿水平轨道向右运动.已知重力加速度为g.
(2009?南充模拟)如图所示是一个设计“过山车”的试验装置的原理示意图,光滑斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R.一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,当它第一次经过B点进入圆形轨道时对轨道的压力为其重力的7倍,小车恰能完成圆周运动并第二次经过最低点沿水平轨道向右运动.已知重力加速度为g. 如图所示是一个设计“过山车”的试验装置的原理示意图,光滑斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R.一个质量为m的小车(可视为质点)从距地面h高处的A点由静止释放沿斜面滑下.已知重力加速度为g.
如图所示是一个设计“过山车”的试验装置的原理示意图,光滑斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R.一个质量为m的小车(可视为质点)从距地面h高处的A点由静止释放沿斜面滑下.已知重力加速度为g.