��Ŀ����
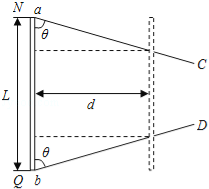
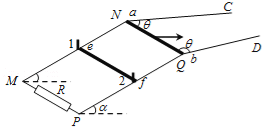
����Ŀ����ͼ��ʾ����������MNC��PQD��MN��PQƽ���Ҽ��ΪL������ƽ����ˮƽ��н�Ϊ����N��Q������MN��ֱ��M��P�������ֵΪR�ĵ��裻�⻬ֱ����NC��QD��ͬһˮƽ���ڣ���NQ�ļнǶ�Ϊ����������Ƚ�����ab��ef������Ϊm������ΪL��ab����ʼλ����ˮƽ��������NQ�غϣ�ef����ֱ������б�����ϣ��뵼���Ķ�Ħ������Ϊ��������С�����ɵ����ϵ�С����1��2�赲����ֹ���ռ��з�����ֱ����ǿ�ų���ͼ��δ�����������������뵼�챣�����ýӴ����������е����ab���ĵ��裬ef������ֵΪR�����Ħ�����뻬��Ħ������С��ȣ����Ը�Ӧ���������Ĵų����������ٶ�Ϊg��
��1�����Ÿ�Ӧǿ�ȴ�СΪB����ab��һ����ֱ��NQ��ˮƽ���ҵ��ٶ�v1����ˮƽ���������˶�������һ�ξ����ֹͣ��ef��ʼ�վ�ֹ����˹���ef���ϲ�����������
��2���ڣ�1���ʹ����У�ab�����о���Ϊd����ͨ��ab��ij�����ĵ�����
��3����ab���Դ�ֱ��NQ���ٶ�v2��ˮƽ���������������˶�������NQλ��ʱȡ��С����1��2�����˶�������ef��ʼ�վ�ֹ�����״̬����ǿ�ų��ĴŸ�Ӧǿ�ȼ��˴ų���ab���˶��������룮����ʾ��![]() ��
��
���𰸡���1��ef���ϲ���������Ϊ![]() ��
��
��2��ͨ��ab��ij�����ĵ���Ϊ![]() ��
��
��3����״̬����ǿ�ų��ĴŸ�Ӧǿ����![]()
![]() ���ų���ab���˶�����������
���ų���ab���˶�����������![]() ��
��
���������⣺��1����ab���ij�����ΪEk��ef���͵���R�ڴ˹��̲��������ֱ�ΪQ��Q1����
Q+Q1=Ek��
��Q=Q1 ��
������ Ek=![]() ��
��
�� Q=![]() ��
��
��2����������Ĺ����У�ab�����е�ʱ��Ϊ��t��ɨ���ĵ��������Ϊ��S��ͨ����S�Ĵ�ͨ��Ϊ������ab�������ĵ綯��ΪE��ab���еĵ���ΪI��ͨ��ab��ij����ĵ����Ϊq����
E=![]() ��
��
������=B��S ��
���� I=![]() ��
��
���� I=![]() ��
��
��ͼ��ʾ����S=d��L��dcot���� ��
��������������ã�q=![]() ��10��
��10��
��3��ab�����о���Ϊxʱ��ab���ڵ����İ���LxΪ��
Lx=L��2xcot�� ��11��
��ʱ��ab�������ĵ綯��ExΪ��E=Bv2Lx ��12��
����ef���ĵ���IxΪ Ix=![]() ��13��
��13��
ef�����ܰ�����FxΪ Fx=BIxL ��14��
������11������14������ã�Fx=![]() ��15��
��15��
�У�15��ʽ�ɵã�Fx��x=0��BΪ���ֵBmʱ�����ֵF1��
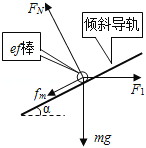
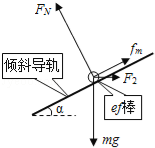
������֪��ab�����ܰ����������ˮƽ����ef�����ܰ����������ˮƽ���ң�ʹF1Ϊ���ֵ������������ͼ��ʾ��
ͼ��fmΪ���Ħ�������У�
F1cos��=mgsin��+����mgcos��+F1sin���� ��16��
������15����16�����ã�Bm=![]()
![]() ��17��
��17��
Bm������Ŀ������ǿ�ų��ĴŸ�Ӧǿ�ȴ�С���ôų��������ֱ���ϣ�Ҳ����ֱ���£�
�У�15��ʽ��֪��BΪBmʱ��Fx��
������15����17����18������
xm=![]()
�𣺣�1��ef���ϲ���������Ϊ![]() ��
��
��2��ͨ��ab��ij�����ĵ���Ϊ![]() ��
��
��3����״̬����ǿ�ų��ĴŸ�Ӧǿ����![]()
![]() ���ų���ab���˶�����������
���ų���ab���˶�����������![]() ��
��