题目内容
12. 如图所示,MN是水平薄板的横截面,其上下两侧均有与MN垂直且与薄板平行的匀强磁场(未画出),上侧磁场的磁感应强度大小为B,下侧磁场的磁感应强度大小为2B,MN上有三个小孔b、c、d,有一带电粒子从位置a开始运动,速度方向与薄板垂直,之后粒子能通过每个小孔.已知ab=bc=cd,粒子从a运动到d的时间为t,不计粒子的重力和孔的尺寸,则该粒子的比荷$\frac{q}{m}$为( )
如图所示,MN是水平薄板的横截面,其上下两侧均有与MN垂直且与薄板平行的匀强磁场(未画出),上侧磁场的磁感应强度大小为B,下侧磁场的磁感应强度大小为2B,MN上有三个小孔b、c、d,有一带电粒子从位置a开始运动,速度方向与薄板垂直,之后粒子能通过每个小孔.已知ab=bc=cd,粒子从a运动到d的时间为t,不计粒子的重力和孔的尺寸,则该粒子的比荷$\frac{q}{m}$为( )| A. | $\frac{3π}{2tB}$ | B. | $\frac{3π}{tB}$ | C. | $\frac{5π}{2tB}$ | D. | $\frac{5π}{tB}$ |
分析 带电粒子垂直射入磁场中,由洛伦兹力提供向心力而做匀速圆周运动,已知ab=bc=cd,画出轨迹,求出周期,由周期公式T=$\frac{2πm}{qB}$求比荷.
解答 解:粒子运动轨迹如图所示:
设粒子在上部的周期为T,则在下部周期为$\frac{T}{2}$;
粒子运动时间:t=1.5T,则:T=$\frac{2}{3}$t,
粒子周期公式:T=$\frac{2πm}{qB}$,
则:$\frac{2πm}{qB}$=$\frac{2}{3}$t,
解得,粒子的比荷:$\frac{q}{m}$=$\frac{3π}{tB}$;
故选:B.
点评 本题考查了带电粒子在匀强磁场匀速圆周运动的问题,关键是画出轨迹,确定时间与周期的关系.

练习册系列答案
相关题目
2.下列说法正确的是 ( )
| A. | 分子间引力和斥力总是随着分子间的距离减小而增大,但引力比斥力变化快 | |
| B. | 物体的内能跟物体的温度和体积有关 | |
| C. | 布朗运动就是液体分子的热运动 | |
| D. | 气体对容器壁的压强是大量气体分子对器壁的碰撞引起的,压强的大小跟气体分子的密集程度以及气体分子的平均动能有关 | |
| E. | 绝热压缩一定质量的气体时气体的温度升高 |
3.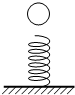 如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
 如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )
如图所示,小球从高处下落到竖直放置的轻弹簧上,在将弹簧压缩到最短的整个过程中,不计空气阻力,下列叙述中正确的是( )| A. | 小球的机械能守恒 | |
| B. | 重力势能和弹性势能之和先减小后增加 | |
| C. | 动能和弹性势能之和先减小后增加 | |
| D. | 重力势能与动能之和始终增大 |
7.已知地球同步卫星的轨道半径是地球半径的k倍,则下列说法正确的是( )
| A. | 第一宇宙速度是同步卫星运行速度的k倍 | |
| B. | 地球表面附近的重力加速度是同步卫星向心加速度的k倍 | |
| C. | 第一宇宙速度是同步卫星运行速度的$\sqrt{k}$倍 | |
| D. | 地球表面附近的重力加速度是同步卫星向心加速度的$\sqrt{k}$倍 |
17. 如图为某台电风扇的铭牌,如果已知该电风扇在额定电压下工作时,转化为机械能的功率等于电动机消耗电功率的97%,则在额定电压下工作时,通过电动机的电流I及电动机线圈的电阻R分别是( )
如图为某台电风扇的铭牌,如果已知该电风扇在额定电压下工作时,转化为机械能的功率等于电动机消耗电功率的97%,则在额定电压下工作时,通过电动机的电流I及电动机线圈的电阻R分别是( )
 如图为某台电风扇的铭牌,如果已知该电风扇在额定电压下工作时,转化为机械能的功率等于电动机消耗电功率的97%,则在额定电压下工作时,通过电动机的电流I及电动机线圈的电阻R分别是( )
如图为某台电风扇的铭牌,如果已知该电风扇在额定电压下工作时,转化为机械能的功率等于电动机消耗电功率的97%,则在额定电压下工作时,通过电动机的电流I及电动机线圈的电阻R分别是( )| A. | I=0.3A,R=711Ω | B. | I=0.3A,R=22Ω | C. | I=3.3A,R=711Ω | D. | I=3.3A,R=22Ω |
4.对分子间相互作用力的理解,下面几种观点正确的是( )(填正确答案)
| A. | 0℃的冰变成0℃的水,体积要减小,表明该过程分子间的作用力为引力 | |
| B. | 0℃的冰变成0℃的水,体积虽减小,但是该过程分子间的作用力为斥力 | |
| C. | 当分子力表现为斥力时,分子势能随分子间距离的减小面增大 | |
| D. | 液体能够流动而固体不能,说明液体分子间作用力小于固体分子间作用力 | |
| E. | 固体发生形变时产生的弹力,本质上是固体大量分子间作用力的宏观表现 |
2.如图甲所示,圆形线圈垂直放在匀强磁场里,规定磁场垂直纸面向外为正方向,磁感应强度随时间变化的关系如图乙所示,下面关于线圈中感应电流的大小和方向的说法正确的是( )


| A. | 第1秒内感应电流增大,电流方向为逆时针 | |
| B. | 第2秒内感应电流大小不变,电流方向为顺时针 | |
| C. | 第3秒内感应电流减小,电流方向为逆时针 | |
| D. | 第4秒内感应电流大小不变,电流方向为顺时针 |
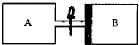 如图所示,导热材料制成的截面积相等,长度均为L=45cm的气缸A、B通过带有阀门的管道连接,初始时阀门K关闭,厚度不计的质量为m=24kg,面积S=20cm2光滑活塞C位于B内下侧,在A内充满压强PA=2×105Pa的理想气体,B内充满压强PB=1×105Pa的同种理想气体,忽略连接气缸的管道体积,室温不变,现打开阀门,求最终平衡时活塞向上移动的距离?
如图所示,导热材料制成的截面积相等,长度均为L=45cm的气缸A、B通过带有阀门的管道连接,初始时阀门K关闭,厚度不计的质量为m=24kg,面积S=20cm2光滑活塞C位于B内下侧,在A内充满压强PA=2×105Pa的理想气体,B内充满压强PB=1×105Pa的同种理想气体,忽略连接气缸的管道体积,室温不变,现打开阀门,求最终平衡时活塞向上移动的距离?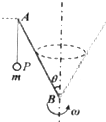 如图所示,长为2l的直杆AB可绕过底端的竖直轴转动,杆与竖直方向的夹角为θ,并保持不变,杆的顶端用长为l的细线挂一小球P,小球的质量为m,若让杆AB绕轴转动的角速度逐渐增大,悬挂小球的细线也将逐渐上摆,己知重力加速度为g.
如图所示,长为2l的直杆AB可绕过底端的竖直轴转动,杆与竖直方向的夹角为θ,并保持不变,杆的顶端用长为l的细线挂一小球P,小球的质量为m,若让杆AB绕轴转动的角速度逐渐增大,悬挂小球的细线也将逐渐上摆,己知重力加速度为g.