题目内容
1.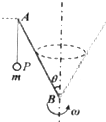 如图所示,长为2l的直杆AB可绕过底端的竖直轴转动,杆与竖直方向的夹角为θ,并保持不变,杆的顶端用长为l的细线挂一小球P,小球的质量为m,若让杆AB绕轴转动的角速度逐渐增大,悬挂小球的细线也将逐渐上摆,己知重力加速度为g.
如图所示,长为2l的直杆AB可绕过底端的竖直轴转动,杆与竖直方向的夹角为θ,并保持不变,杆的顶端用长为l的细线挂一小球P,小球的质量为m,若让杆AB绕轴转动的角速度逐渐增大,悬挂小球的细线也将逐渐上摆,己知重力加速度为g.(1)杆AB绕轴开始转动后,在某一角速度下,细线能不能保持竖直与水平两种状态?试简述理由.
(2)当细线与杆AB刚好垂直时,杆绕轴转动的角速度多大?
分析 (1)小球随同杆转动,将在以杆上某点为圆心的水平面内做匀速圆周运动,小球只可能受重力和细线的拉力;
(2)根据几何关系求出半径,小球在竖直方向受力平衡,在水平方向合力提供向心力,根据向心力公式求解.
解答 解:小球随同杆转动,将在以杆上某点为圆心的水平面内做匀速圆周运动,小球只可能受重力和细线的拉力.若细线竖直,则两力都是竖直方向,无法提供小球做圆周运动的向心力,所以细线不能保持竖直状态;若细线水平,则细线拉力可提供向心力,但在竖直方向上小球受重力作用无法保持平衡,所以细线也不能保持水平状态.
(2)当细线与杆AB刚好垂直时,小球做匀速圆周运动的半径为:
r=lcosθ+2lsinθ
设细线对小球的拉力为F,在竖直方向上,有:
Fsinθ=mg
在水平方向上,由向心力公式有:
Fcosθ=mrω2
解得:$ω=\sqrt{\frac{g}{l(1+2tanθ)sinθ}}$
答:(1)若细线竖直,则两力都是竖直方向,无法提供小球做圆周运动的向心力,所以细线不能保持竖直状态;若细线水平,则细线拉力可提供向心力,但在竖直方向上小球受重力作用无法保持平衡,所以细线也不能保持水平状态..
(2)当细线与杆AB刚好垂直时,杆绕轴转动的角速度为$\sqrt{\frac{g}{l(1+2tanθ)sinθ}}$.
点评 解决本题的关键搞清小球向心力的来源,运用牛顿第二定律进行求解,要求同学们能正确分析物体的受力情况,难度适中.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
12. 如图所示,MN是水平薄板的横截面,其上下两侧均有与MN垂直且与薄板平行的匀强磁场(未画出),上侧磁场的磁感应强度大小为B,下侧磁场的磁感应强度大小为2B,MN上有三个小孔b、c、d,有一带电粒子从位置a开始运动,速度方向与薄板垂直,之后粒子能通过每个小孔.已知ab=bc=cd,粒子从a运动到d的时间为t,不计粒子的重力和孔的尺寸,则该粒子的比荷$\frac{q}{m}$为( )
如图所示,MN是水平薄板的横截面,其上下两侧均有与MN垂直且与薄板平行的匀强磁场(未画出),上侧磁场的磁感应强度大小为B,下侧磁场的磁感应强度大小为2B,MN上有三个小孔b、c、d,有一带电粒子从位置a开始运动,速度方向与薄板垂直,之后粒子能通过每个小孔.已知ab=bc=cd,粒子从a运动到d的时间为t,不计粒子的重力和孔的尺寸,则该粒子的比荷$\frac{q}{m}$为( )
 如图所示,MN是水平薄板的横截面,其上下两侧均有与MN垂直且与薄板平行的匀强磁场(未画出),上侧磁场的磁感应强度大小为B,下侧磁场的磁感应强度大小为2B,MN上有三个小孔b、c、d,有一带电粒子从位置a开始运动,速度方向与薄板垂直,之后粒子能通过每个小孔.已知ab=bc=cd,粒子从a运动到d的时间为t,不计粒子的重力和孔的尺寸,则该粒子的比荷$\frac{q}{m}$为( )
如图所示,MN是水平薄板的横截面,其上下两侧均有与MN垂直且与薄板平行的匀强磁场(未画出),上侧磁场的磁感应强度大小为B,下侧磁场的磁感应强度大小为2B,MN上有三个小孔b、c、d,有一带电粒子从位置a开始运动,速度方向与薄板垂直,之后粒子能通过每个小孔.已知ab=bc=cd,粒子从a运动到d的时间为t,不计粒子的重力和孔的尺寸,则该粒子的比荷$\frac{q}{m}$为( )| A. | $\frac{3π}{2tB}$ | B. | $\frac{3π}{tB}$ | C. | $\frac{5π}{2tB}$ | D. | $\frac{5π}{tB}$ |
9.在研究天体运动中,发现万有引力定律和测出引力常量的科学家分别是( )
| A. | 第谷、开普勒 | B. | 伽利略、迪卡尔 | C. | 牛顿、卡文迪许 | D. | 牛顿、开普勒 |
16.质量相等的A、B两物体,从等高处同时开始运动,A做自由落体运动,B做平抛运动,不计空气阻力,则关于两物体在落地前的运动关系,下列结论正确的是( )
| A. | 在任何对刻两物体总在同一水平面上 | |
| B. | 在任何时刻两物体总在同一竖直面上 | |
| C. | 两物体在相同时间内发生的位移相等 | |
| D. | 在相等时间内两物体的速度变化相等 |
6.如图所示,紧贴圆筒内壁上的物体,随圆筒一起做匀速圆周运动,物体所需的向心力的来源为( )

| A. | 重力 | B. | 弹力 | ||
| C. | 静摩擦力 | D. | 重力与弹力的合力 |
13.卫星发射中心反射等质量的两颗圆轨道卫星,其中一颗卫星的轨道半径为2.8×107m.另一颗的轨道半径为4.2×107m,两卫星相比,前一颗卫星的( )
| A. | 向心力较小 | B. | 向心加速度较大 | ||
| C. | 绕地球的运动速率较大 | D. | 绕地球转动的周期较大 |
10. 可用如图所示的实验装置来探究影响平行板电容器电容的因素,其中电容器左侧极板和静电剂外壳接地,电容器右侧极板与静电计金属球相连,在实验过程中电容器的带电量保持不变,则下列说法正确的是( )
可用如图所示的实验装置来探究影响平行板电容器电容的因素,其中电容器左侧极板和静电剂外壳接地,电容器右侧极板与静电计金属球相连,在实验过程中电容器的带电量保持不变,则下列说法正确的是( )
 可用如图所示的实验装置来探究影响平行板电容器电容的因素,其中电容器左侧极板和静电剂外壳接地,电容器右侧极板与静电计金属球相连,在实验过程中电容器的带电量保持不变,则下列说法正确的是( )
可用如图所示的实验装置来探究影响平行板电容器电容的因素,其中电容器左侧极板和静电剂外壳接地,电容器右侧极板与静电计金属球相连,在实验过程中电容器的带电量保持不变,则下列说法正确的是( )| A. | 将左侧极板向上平移一小段距离,静电计指针张角变小 | |
| B. | 将左侧极板向右平移一小段距离,静电计指针张角变小 | |
| C. | 将左侧极板向左平移一小段距离,静电计指针张角变小 | |
| D. | 在极板间插入某种电介质,静电计指针张角变小 |
 频闪摄影是研究变速运动常用的实验手段,在暗室中照相机的快门处于常开状态,频闪仪每隔一定时间发出一次短暂的强烈闪光,照亮运动的物体,于是胶片上记录了物体在几个闪光时刻的位置.如图是质量为0.1kg的小球自由下落时的频闪照片(照片中的数字是小球距起点的距离,单位:cm),频闪仪每隔0.04s闪光一次.某同学根据这张频闪照片验证机械能守恒定律,已知当地的重力加速度大小为9.8m/s2,则:
频闪摄影是研究变速运动常用的实验手段,在暗室中照相机的快门处于常开状态,频闪仪每隔一定时间发出一次短暂的强烈闪光,照亮运动的物体,于是胶片上记录了物体在几个闪光时刻的位置.如图是质量为0.1kg的小球自由下落时的频闪照片(照片中的数字是小球距起点的距离,单位:cm),频闪仪每隔0.04s闪光一次.某同学根据这张频闪照片验证机械能守恒定律,已知当地的重力加速度大小为9.8m/s2,则: 用油膜法估测分值的大小方法及步骤如下:
用油膜法估测分值的大小方法及步骤如下: