题目内容
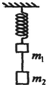
如图所示,弹簧的劲度系数k=10N/m,弹簧下面挂着质量分别为m1=0.5kg和m2=0.3kg的两个物体,开始时它们都处于静止状态.突然把m1和m2的连线剪断后,m1的最大速率是(弹性势能的表达式是E=
k△x2,其中△x为形变量)( )
| 1 |
| 2 |
| A.0.77m/s | B.0.98m/s | C.1.34m/s | D.1.94m/s |

没有剪短细线时,弹簧的伸长量,由胡克定律得:x1=
=
m=0.8m
剪短细线后,弹簧的伸长量为:x2=0.5m
m1的最大速率位于弹簧的平衡位置处,所以弹簧弹性势能的减少量等于动能的增加量和重力势能的增加量
即
k(
-
)=
mv2+mg(x1-x2)
代入数据解之得:v=1.34m/s,故ABD错误,C正确.
故选:C.
| (m1+m2)g |
| k |
| 8 |
| 10 |
剪短细线后,弹簧的伸长量为:x2=0.5m
m1的最大速率位于弹簧的平衡位置处,所以弹簧弹性势能的减少量等于动能的增加量和重力势能的增加量
即
| 1 |
| 2 |
| x | 21 |
| x | 22 |
| 1 |
| 2 |
代入数据解之得:v=1.34m/s,故ABD错误,C正确.
故选:C.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
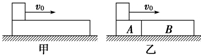
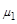 ,与CB段间的动摩擦因数为
,与CB段间的动摩擦因数为 。
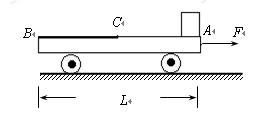
。
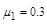 ,m=1kg,求水平恒力F的大小;
,m=1kg,求水平恒力F的大小;

 滑上B的左端,在右端与B碰撞后,最后恰好滑回木板B的左端. 已知
滑上B的左端,在右端与B碰撞后,最后恰好滑回木板B的左端. 已知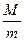 =3,并且在A与挡板碰撞时无机械能损失,忽略碰撞时间,取g=10m/s2,求:
=3,并且在A与挡板碰撞时无机械能损失,忽略碰撞时间,取g=10m/s2,求:
