题目内容
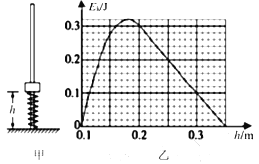
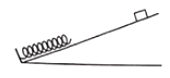
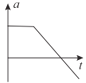
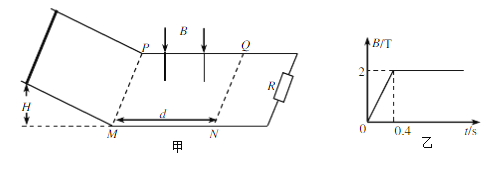
【题目】如图,两相互平行的光滑金属导轨,相距L=0.2m,左侧轨道的倾角θ=30°,M、P是倾斜轨道与水平轨道连接点,水平轨道右端接有电阻R=1.5Ω,MP、NQ之间距离d=0.8m,且在MP、NQ间有宽与导轨间距相等的方向竖直向下的匀强磁场,磁感应强度B随时间t变化关系如图乙所示,-质量m=0.01kg、电阻r=0.5Ω的导体棒在t=0时刻从左侧轨道高H=0.2m处静止释放,下滑后平滑进入水平轨道(转角处天机械能损失)。导体棒始终与导轨垂直并接触良好,轨道的电阻和电感不计,g取10m/s2。求:
(1)导体棒从释放到刚进入磁场所用的时间t;
(3)导体棒在水平轨道上的滑行距离d;
(2)导体棒从释放到停止的过程中,电阻R上产生的焦耳热。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)0.111J
;(3)0.111J
【解析】
(1)设导体棒进入磁场前瞬间速度大小为![]() ,导体棒从释放到刚进入磁场的过程中,由机械能守恒定律有
,导体棒从释放到刚进入磁场的过程中,由机械能守恒定律有
![]()
解得
![]()
根据位移公式有
![]()
解得
![]()
导体棒从释放到刚进入磁场所用的时间为0.4s。
(2)导体棒进入磁场到静止,由动量定理得
![]()
根据安培力公式有
![]()
又
![]()
联立得
![]()
通过导体棒的电荷量为
![]()
![]()
联立解得
![]()
导体棒在水平轨道上的滑行距离为0.25m。
(3)导体棒滑入磁场之前![]() 上产生的焦耳热为
上产生的焦耳热为
![]()
由法拉第电磁感定律有
![]()
由闭合电路欧姆定律
![]()
可得
![]()
根据能量守恒可知,导体棒进入磁场后的总热量
![]()
又
![]()
解得
![]()
故电阻![]() 上产生的焦耳热为
上产生的焦耳热为
![]()
故总热量为0.111J。

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目