题目内容
 如图所示,ABC是三棱镜的一个截面,其折射率为n=1.5.现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点,AN=NB=2cm,入射角的大小为i,且sini=0.75.已知真空中的光速c=3.0×108m/s,求:
如图所示,ABC是三棱镜的一个截面,其折射率为n=1.5.现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点,AN=NB=2cm,入射角的大小为i,且sini=0.75.已知真空中的光速c=3.0×108m/s,求:①光在棱镜中传播的速率;
②此束光进入棱镜后从棱镜射出的方向和位置.(不考虑AB面的反射.
分析:光在棱镜中传播的速率应根据公式v=
求解.
已知折射率n和入射角的正弦sini,根据折射定律n=
求出折射角.由公式sinC=
求得临界角C.由几何知识求出光线射到BC面的入射角,根据入射角与临界角的大小关系,判断光线在BC面上能否发生全反射,再进一步确定此束光线射出棱镜后的方向.
| c |
| n |
已知折射率n和入射角的正弦sini,根据折射定律n=
| sini |
| sinr |
| 1 |
| n |
解答: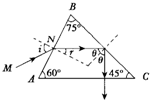 解:①光在棱镜中传播的速率为 v=
解:①光在棱镜中传播的速率为 v=
=2×108m/s
②由题光在AB面上入射角的正弦sini=sinθ1=0.75,由折射定律得
n=
得:sinr=
=0.5,得r=30°
由几何关系得,光线在BC面上的入射角θ=45°
设临界角为C,则由sinC=
得
sinC=
<
可知C<45°
则光线在BC面的入射角θ>C
故光线在BC面上发生全反射后,根据几何知识和反射定律得知,光线垂直AC面射出棱镜.
答:①光在棱镜中传播的速率是2×108m/s,
②此束光线射出棱镜后的方向垂直AC面.
 解:①光在棱镜中传播的速率为 v=
解:①光在棱镜中传播的速率为 v=| c |
| n |
②由题光在AB面上入射角的正弦sini=sinθ1=0.75,由折射定律得
n=
| sini |
| sinr |
得:sinr=
| sini |
| n |
由几何关系得,光线在BC面上的入射角θ=45°
设临界角为C,则由sinC=
| 1 |
| n |
sinC=
| 2 |
| 3 |
| ||
| 2 |
可知C<45°
则光线在BC面的入射角θ>C
故光线在BC面上发生全反射后,根据几何知识和反射定律得知,光线垂直AC面射出棱镜.
答:①光在棱镜中传播的速率是2×108m/s,
②此束光线射出棱镜后的方向垂直AC面.
点评:本题是折射定律、光速公式和全反射知识的综合应用.当光从光密介质射入光疏介质时要考虑能否发生全反射.

练习册系列答案
相关题目
 如图所示,ABC为光滑轨道,其中AB段水平放置,BC段是半径为R的圆弧,AB与BC相切于B点.A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧牌原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处但无挤压.现使一质量为m的小球从圆孤轨道上距水平轨道高h处的D点由静止开始下滑,小球与物块相碰后立即共速但不粘连,物块与L形挡板相碰后速度立即减为零也不粘连.(整个过程中,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g)
如图所示,ABC为光滑轨道,其中AB段水平放置,BC段是半径为R的圆弧,AB与BC相切于B点.A处有一竖直墙面,一轻弹簧的一端固定于墙上,另一端与一质量为M的物块相连接,当弹簧牌原长状态时,物块恰能与固定在墙上的L形挡板相接触于B处但无挤压.现使一质量为m的小球从圆孤轨道上距水平轨道高h处的D点由静止开始下滑,小球与物块相碰后立即共速但不粘连,物块与L形挡板相碰后速度立即减为零也不粘连.(整个过程中,弹簧没有超过弹性限度,不计空气阻力,重力加速度为g) 如图所示,ABC三个木块的质量均为m,置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触但不连接,现将弹簧压缩一些后,用细线把BC系住,使之处于静止状态.让A以初速度v0沿BC的连线方向朝B运动,与B相碰并粘合在一起,之后立即断开细线,已知弹簧恢复原长时C的速度为v0,求弹簧释放的弹性势能是多少?
如图所示,ABC三个木块的质量均为m,置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触但不连接,现将弹簧压缩一些后,用细线把BC系住,使之处于静止状态.让A以初速度v0沿BC的连线方向朝B运动,与B相碰并粘合在一起,之后立即断开细线,已知弹簧恢复原长时C的速度为v0,求弹簧释放的弹性势能是多少?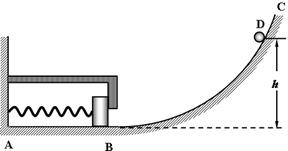

 (3)如图所示,ABC为直角三棱镜,BC边长为16 cm,AB边长为32 cm,有一束很强的细光束OP射到BC边上,入射点P为BC的中点,OP与BC的夹角为30°,该光束从P点进入棱镜后再经AC面反射沿与AC平行的MN方向射出,其中M为AC边上的一点,AM=8cm。准确作出棱镜内部的光路图(不必写出作图过程),注明并求出棱镜的折射率是多少?
(3)如图所示,ABC为直角三棱镜,BC边长为16 cm,AB边长为32 cm,有一束很强的细光束OP射到BC边上,入射点P为BC的中点,OP与BC的夹角为30°,该光束从P点进入棱镜后再经AC面反射沿与AC平行的MN方向射出,其中M为AC边上的一点,AM=8cm。准确作出棱镜内部的光路图(不必写出作图过程),注明并求出棱镜的折射率是多少?

 倍
倍
 (3)如图所示,ABC为直角三棱镜,BC边长为16 cm,AB边长为32 cm,有一束很强的细光束OP射到BC边上,入射点P为BC的中点,OP与BC的夹角为30°,该光束从P点进入棱镜后再经AC面反射沿与AC平行的MN方向射出,其中M为AC边上的一点,AM=8cm。准确作出棱镜内部的光路图(不必写出作图过程),注明并求出棱镜的折射率是多少?
(3)如图所示,ABC为直角三棱镜,BC边长为16 cm,AB边长为32 cm,有一束很强的细光束OP射到BC边上,入射点P为BC的中点,OP与BC的夹角为30°,该光束从P点进入棱镜后再经AC面反射沿与AC平行的MN方向射出,其中M为AC边上的一点,AM=8cm。准确作出棱镜内部的光路图(不必写出作图过程),注明并求出棱镜的折射率是多少?