题目内容
 如图所示,ABC三个木块的质量均为m,置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触但不连接,现将弹簧压缩一些后,用细线把BC系住,使之处于静止状态.让A以初速度v0沿BC的连线方向朝B运动,与B相碰并粘合在一起,之后立即断开细线,已知弹簧恢复原长时C的速度为v0,求弹簧释放的弹性势能是多少?
如图所示,ABC三个木块的质量均为m,置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触但不连接,现将弹簧压缩一些后,用细线把BC系住,使之处于静止状态.让A以初速度v0沿BC的连线方向朝B运动,与B相碰并粘合在一起,之后立即断开细线,已知弹簧恢复原长时C的速度为v0,求弹簧释放的弹性势能是多少?分析:A与B碰撞过程中动量守恒,由动量守恒定律可以求出碰后AB的共同速度;线断开,A、B、C组成的系统中动量守恒,由动量守恒定律可以列方程求出弹簧恢复原长时AB的速度;在弹簧弹开过程中,系统机械能守恒,由机械能守恒定律可以列方程,解方程即可求出弹簧释放的弹性势能.
解答:解:(1)设碰后A、B的共同速度的大小为v1,以AB组成的系统为研究对象,由动量守恒定律得:
mv0=2mv1,
得:v1=0.5mv0;
设弹簧恢复原长时,A、B的速度大小为v2,A、B、C组成的系统中动量守恒,则得:
mv0=2mv2+mv0,
解得:v2=0;
设弹簧释放的弹性势能为EP,从细线断开到C与弹簧分开的过程中,三个物体组成的系统机械能守恒,则有:
EP+
?2m
=
?2m
+
m
代入解得,EP=
.
答:弹簧释放的弹性势能是
.
mv0=2mv1,
得:v1=0.5mv0;
设弹簧恢复原长时,A、B的速度大小为v2,A、B、C组成的系统中动量守恒,则得:
mv0=2mv2+mv0,
解得:v2=0;
设弹簧释放的弹性势能为EP,从细线断开到C与弹簧分开的过程中,三个物体组成的系统机械能守恒,则有:
EP+
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 0 |
代入解得,EP=
| 1 |
| 4 |
| m | 2 0 |
答:弹簧释放的弹性势能是
| 1 |
| 4 |
| m | 2 0 |
点评:分析清楚物体运动过程,熟练应用动量守恒定律、机械能守恒定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一质点做平抛运动,部分轨迹如图所示,ABC三点为质点在轨迹上的连续三个闪光照像的位置,每个小正方格的边长为10cm,若本地的重力加速度g=10m/s2,求质点做平抛运动的水平初速度v0的大小.
一质点做平抛运动,部分轨迹如图所示,ABC三点为质点在轨迹上的连续三个闪光照像的位置,每个小正方格的边长为10cm,若本地的重力加速度g=10m/s2,求质点做平抛运动的水平初速度v0的大小.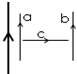 一通有恒定电流的长直导线周围放置了abc三根完全相同的导体棒,导体棒通有大小相同的电流,电流的方向及导体棒的分布如图所示,关于三个导体棒受到长直导线磁场力的说法正确的是( )
一通有恒定电流的长直导线周围放置了abc三根完全相同的导体棒,导体棒通有大小相同的电流,电流的方向及导体棒的分布如图所示,关于三个导体棒受到长直导线磁场力的说法正确的是( )