题目内容
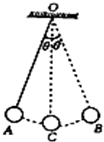 质量为m、带电量为+q的小球,用一绝缘细线悬挂于O点,开始时它在A、B之间来回摆动,OA、OB与竖直方向OC的夹角均为θ如图所示.求:
质量为m、带电量为+q的小球,用一绝缘细线悬挂于O点,开始时它在A、B之间来回摆动,OA、OB与竖直方向OC的夹角均为θ如图所示.求:(1)如果当它摆到B点时突然施加一竖直向上的、大小为E=
| mg | q |
(2)如果这一电场是在小球从A点摆到最低点C时突然加上去的,则当小球运动到B点时线中的拉力T2.
分析:(1)在B点时,小球的速度为零,加上电场后,电场力与重力平衡,物体保持静止,根据平衡条件求解线中拉力T1;
(2)在最低点C加电场后,电场力与重力平衡,物体做匀速圆周运动,由拉力提供向心力,根据牛顿第二定律求解线中的拉力T2.
(2)在最低点C加电场后,电场力与重力平衡,物体做匀速圆周运动,由拉力提供向心力,根据牛顿第二定律求解线中的拉力T2.
解答:解:(1)小球所受的电场力大小 F=qE=mg,方向竖直向上,故电场力与重力平衡;运动到最高点B时加电场后,小球保持静止,故细线的拉力 T1=0;
(2)如果这一电场是在小球从A点摆到最低点C时突然加上去的,由于重力与电场力平衡,故此后小球做匀速圆周运动,由线的拉力提供向心力,而且线的拉力大小不变,根据牛顿第二定律,有:
T2=m
从A到C过程,根据动能定理,有:
mgL(1-cosθ)=
mv2
联立解得:
T2=2(1-cosθ)mg
答:(1)此时线中拉力T1为0;(2)当小球运动到B点时线中的拉力T2大小为2(1-cosθ)mg.
(2)如果这一电场是在小球从A点摆到最低点C时突然加上去的,由于重力与电场力平衡,故此后小球做匀速圆周运动,由线的拉力提供向心力,而且线的拉力大小不变,根据牛顿第二定律,有:
T2=m
| v2 |
| L |
从A到C过程,根据动能定理,有:
mgL(1-cosθ)=
| 1 |
| 2 |
联立解得:
T2=2(1-cosθ)mg
答:(1)此时线中拉力T1为0;(2)当小球运动到B点时线中的拉力T2大小为2(1-cosθ)mg.
点评:本题考查了平衡条件、圆周运动向心力公式及动能定理的直接应用,关键要求同学们能正确对小球进行受力分析,再选择合适的规律解题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目

 真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m,带电量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻物体在轨迹最低点且重力势能为零,电势能也为零,那么,下列说法正确的是( )
真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m,带电量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻物体在轨迹最低点且重力势能为零,电势能也为零,那么,下列说法正确的是( ) 如图所示,空中有水平向右的匀强电场和垂直于纸面向外的匀强磁场,质量为m,带电量为+q的滑块沿水平向右做匀速直线运动,滑块和水平面间的动摩擦因数为μ,滑块与墙碰撞后速度为原来的一半.滑块返回时,去掉了电场,恰好也做匀速直线运动,求原来电场强度的大小.
如图所示,空中有水平向右的匀强电场和垂直于纸面向外的匀强磁场,质量为m,带电量为+q的滑块沿水平向右做匀速直线运动,滑块和水平面间的动摩擦因数为μ,滑块与墙碰撞后速度为原来的一半.滑块返回时,去掉了电场,恰好也做匀速直线运动,求原来电场强度的大小. 如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上缘有一个质量为m,带电量为+q的小球,由静止开始由半圆形轨道的顶点沿轨道运动,下列说法正确的是( )
如图所示,绝缘光滑的半圆轨道位于竖直平面,竖直向下的匀强电场E穿过其中,在轨道的上缘有一个质量为m,带电量为+q的小球,由静止开始由半圆形轨道的顶点沿轨道运动,下列说法正确的是( )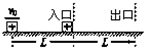 如图所示,在宽度为L的两虚线区域内存在匀强电场,一质量为m,带电量为+q的滑块(可看成点电荷),从距该区域为L的绝缘水平面上以初速度v0向右运动并进入电场区域,滑块与水平面间的动摩擦因数为μ.
如图所示,在宽度为L的两虚线区域内存在匀强电场,一质量为m,带电量为+q的滑块(可看成点电荷),从距该区域为L的绝缘水平面上以初速度v0向右运动并进入电场区域,滑块与水平面间的动摩擦因数为μ.