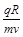题目内容
 真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m,带电量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻物体在轨迹最低点且重力势能为零,电势能也为零,那么,下列说法正确的是( )
真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m,带电量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻物体在轨迹最低点且重力势能为零,电势能也为零,那么,下列说法正确的是( )分析:物体做匀速圆周运动,受重力、电场力和洛伦兹力,其中重力和电场力平衡,洛伦兹力提供向心力.
解答:解:A、重力与电场力平衡,故电场力向上,由于电场方向向上,故电荷带正电;由于磁场方向垂直向内,根据左手定则可以判断电荷逆时针方向转动,故A正确;
B、洛伦兹力不做功,只有重力和电场力做功,故只有机械能和电势能相互转化,总量守恒,在最低点时,有E=
mv2,故B错误;
C、重力势能的表达式为:Ep=mg(R-Rcosθ)=mgR(1-cosωt)=mgR(1-cos
t),故C正确;
D、电势能和重力势能总量守恒,故电势能为:Ep′=-Ep=-mg(R-Rcosθ)=-mgR(1-cosωt)=-mgR(1-cos
t),故D正确;
故选ACD.
B、洛伦兹力不做功,只有重力和电场力做功,故只有机械能和电势能相互转化,总量守恒,在最低点时,有E=
| 1 |
| 2 |
C、重力势能的表达式为:Ep=mg(R-Rcosθ)=mgR(1-cosωt)=mgR(1-cos
| v |
| R |
D、电势能和重力势能总量守恒,故电势能为:Ep′=-Ep=-mg(R-Rcosθ)=-mgR(1-cosωt)=-mgR(1-cos
| v |
| R |
故选ACD.
点评:本题关键明确重力和电场力平衡,洛伦兹力提供向心力,然后列式分析求解,不难.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
 如图所示,真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m、带电荷量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动,下列说法正确的是( )
如图所示,真空中存在竖直向上的匀强电场和水平方向的匀强磁场,一质量为m、带电荷量为q的物体以速度v在竖直平面内做半径为R的匀速圆周运动,下列说法正确的是( )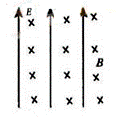

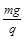 B.物体运动过程中机械能守恒
B.物体运动过程中机械能守恒