题目内容
在北戴河旅游景点之一的滑沙场有两个坡度不同的滑道AB和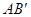 ,(均可看作斜面),甲、乙两名质量相等的旅游者分别乘两个完全相同的滑沙橇从A点由静止开始分别沿AB和
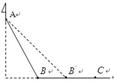
,(均可看作斜面),甲、乙两名质量相等的旅游者分别乘两个完全相同的滑沙橇从A点由静止开始分别沿AB和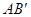 滑下,最后都停在水平沙面BC上,如图所示。设滑沙橇和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认圆滑的,滑沙者保持姿势坐在滑沙橇上不动.则下列说法中正确的是:
滑下,最后都停在水平沙面BC上,如图所示。设滑沙橇和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认圆滑的,滑沙者保持姿势坐在滑沙橇上不动.则下列说法中正确的是:
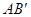 ,(均可看作斜面),甲、乙两名质量相等的旅游者分别乘两个完全相同的滑沙橇从A点由静止开始分别沿AB和
,(均可看作斜面),甲、乙两名质量相等的旅游者分别乘两个完全相同的滑沙橇从A点由静止开始分别沿AB和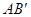 滑下,最后都停在水平沙面BC上,如图所示。设滑沙橇和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认圆滑的,滑沙者保持姿势坐在滑沙橇上不动.则下列说法中正确的是:
滑下,最后都停在水平沙面BC上,如图所示。设滑沙橇和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认圆滑的,滑沙者保持姿势坐在滑沙橇上不动.则下列说法中正确的是:
A.甲在B点的动能一定大于乙在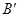 点的动能 点的动能 |
| B.甲滑行的总路程一定大于乙滑行的总路程 |
| C.甲在斜面上滑行时克服摩擦力做功多 |
| D.甲全部滑行的水平位移一定等于乙全部滑行的水平位移 |
ABD
试题分析: 滑沙者在由斜面滑到水平面的过程中,由动能定理,设滑道的倾角为θ,动摩擦因数为
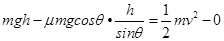 ,即得:
,即得: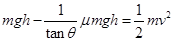 ,由于AB′与水平面的夹角小于AB与水平面的夹角,所以得知甲在B点的动能大于乙在B′点的动能.故A正确.对全程使用动能定理可得:
,由于AB′与水平面的夹角小于AB与水平面的夹角,所以得知甲在B点的动能大于乙在B′点的动能.故A正确.对全程使用动能定理可得: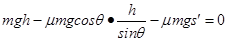 ,得到
,得到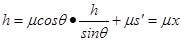 ,所以水平位移
,所以水平位移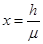 ,即两者的水平位移相同,,与斜面的倾角无关,所以他们将停在离出发点水平位移相同的位置,则几何知识可知,甲的滑行总路程比乙长.故BD正确,在斜面上滑行时,有:
,即两者的水平位移相同,,与斜面的倾角无关,所以他们将停在离出发点水平位移相同的位置,则几何知识可知,甲的滑行总路程比乙长.故BD正确,在斜面上滑行时,有: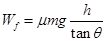 ,所以甲克服的摩擦力做功小,C错误
,所以甲克服的摩擦力做功小,C错误故选ABD
点评:本题应用动能定理分析两人的速度关系和水平位移关系,得到的结论:两人滑行的水平位移与斜面的倾角无关,是一个重要的经验结论,在理解的基础上进行记忆.

练习册系列答案
相关题目
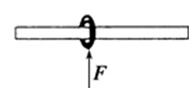
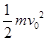
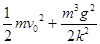
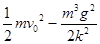
 ,求:
,求:
 mvm2-
mvm2-


 ,从此刻起在AB区域内加上一个水平向左的强度不变的有界匀强电场(区域外不存在电场)。若小滑块受到的电场力与滑动摩擦力大小相等,则滑块离开AB区域时的速度 ,要使小滑块在AB区域内运动的时间达到最长,电场强度应为 。(设最大静摩擦力大小等于滑动摩擦力)
,从此刻起在AB区域内加上一个水平向左的强度不变的有界匀强电场(区域外不存在电场)。若小滑块受到的电场力与滑动摩擦力大小相等,则滑块离开AB区域时的速度 ,要使小滑块在AB区域内运动的时间达到最长,电场强度应为 。(设最大静摩擦力大小等于滑动摩擦力)