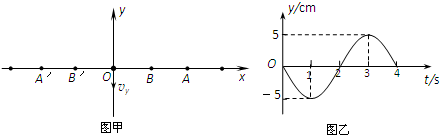题目内容
 如图甲所示,一根水平张紧的弹性长绳上有等间距的Q′、P′、O、P、Q质点,相邻两质点间距离为1m,t=0时刻O质点从平衡位置开始沿y轴正方向振动,并分别产生向左和向右传播的机械波,O质点振动图象如图乙所示.当O质点第一次达到正方向最大位移时,P点刚开始振动,则( )
如图甲所示,一根水平张紧的弹性长绳上有等间距的Q′、P′、O、P、Q质点,相邻两质点间距离为1m,t=0时刻O质点从平衡位置开始沿y轴正方向振动,并分别产生向左和向右传播的机械波,O质点振动图象如图乙所示.当O质点第一次达到正方向最大位移时,P点刚开始振动,则( )分析:由题意,波源O产生两列波,同时向左和向右传播,利用对称性,分析P、P′的振动步调.根据Q′的振动情况,确定时间,求出O点运动路程.根据振动图象求周期,由O点的起振情况求出波长,再求出波速.
解答:解:A、根据对称性,P与P′步调始终一致.故A错误.
B、Q′起振方向与O点起振方向相同:向上,当Q′点振动第一次达到负向最大位移时,经过
T时间,而波由O点传到Q时间为
T,则质点通过路程为s=5A=25cm.故B正确.
C、由振动图象得知,T=4s,由O点起振情况得λ=4m,则v=
=1m/s,故C正确.
D、波速由介质的性质决定,故D错误.
故选BCD
B、Q′起振方向与O点起振方向相同:向上,当Q′点振动第一次达到负向最大位移时,经过
| 3 |
| 4 |
| 1 |
| 2 |
C、由振动图象得知,T=4s,由O点起振情况得λ=4m,则v=
| λ |
| T |
D、波速由介质的性质决定,故D错误.
故选BCD
点评:本题解题要注意对称性.质点通过的路程往往根据下面的结论确定:质点在一个周期内,通过路程4A,半个周期内通过路程2A.但其他情况,不能类推.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目