��Ŀ����
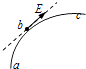
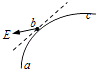
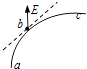
����Ŀ����ͼ��ʾ�����ʹ���ˮƽ��֮��ļн�Ϊ��=37��ǣ���v=2m/s�ĺ㶨������ʱ��ת����һ������Ϊm=1kg�������Գ��ٶ�v0=10m/s�Ӵ��ʹ�����A��B֮����е㿪ʼ�ش��ʹ������˶�����֪�����봫�ʹ�֮��Ķ�Ħ������Ϊ��=0.5��A��B֮��ľ���ΪL=20.4m����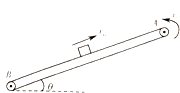
��1�������ش��ʹ������˶���������Ϊ���٣�
��2�������ڴ��ʹ����˶�����ʱ��Ϊ���٣�
��3�������ڴ��ʹ�����Դ��ʹ����ߵ���·��Ϊ���٣�
��4�������ڴ��ʹ�������Ħ��������������Ϊ���٣���g=10m/s2 �� sin37��=0.6��cos37��=0.8��
���𰸡�
��1��
�⣺���徭��ʱ��t1�ش��ʹ������˶��ٶ�Ϊ�㣬��ʱ��t1�ڣ������λ��Ϊx1�����ʹ�λ��Ϊx2��
�����壬�У�mgsin��+��mgcos��=ma1
v0=a1t1
x1= ![]() a1t12
a1t12
�Դ��ʹ����У�x2=vt1
�����������ã�a1=10m/s2��t1=1s��x1=5m��x2=2m
��2��
�⣺���徭��ʱ��t2�ش��ʹ������˶��ٶȺʹ��ʹ����٣���ʱ��t2�ڣ������λ��Ϊx3�����ʹ�λ��Ϊx4���˹������������������䣬���ٶ�Ϊa1����
�����壬�У�v=a1t2
x3= ![]() a1t22
a1t22
�Դ��ʹ����У�x4=vt2
�����������ã�t2=0.2s��x3=0.2m��x4=0.4m
���徭��ʱ��t3�ش��ʹ�����ǡ���뿪���ʹ������뿪ʱ�ٶ�Ϊv�䣬��ʱ��t3�ڣ������λ��Ϊx5�����ʹ�λ��Ϊx6��
�����壬�У�mgsin�ȩ���mgcos��=ma2
v��=v+a2t3
x5=vt3+ ![]() a2t32
a2t32
�Դ��ʹ����У�x6=vt3
������֪��x5= ![]() +x1��x3
+x1��x3
�����������ã�a2=2m/s2��x5=15m��t3=3s��x6=6m��v��=8m/s��
�������ڴ��ʹ����˶�����ʱ��Ϊt���У�
t=t1+t2+t3
��ã�t=4.2s
��3��
�⣺�������ڴ��ʹ�����Դ��ʹ��˶�����·��Ϊx���У�
x=�� x1+x2��+�� x4��x3��+��x5��x6��
��ã�x=16.2m
��4��
�⣺�������ڴ��ʹ�������Ħ��������������ΪQ���У�
Q=��mgxcos��
��ã�Q=64.8J
���������������������ȼ���ֱ���˶����ٶȼ�Ϊ������ȼ���ֱ���˶����ٶȺʹ��ʹ���Ⱥ��������������������ж�������˶��������ţ�ٵڶ����ɼ��˶�ѧ���ɷ���������⣬����Q=��mg��x��������������
�����㾫����ͨ��������ù��ܹ�ϵ�����յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1�����Խ����⣮

 С�����ϵ�д�
С�����ϵ�д�