题目内容
16. 如图所示,吊车以恒定速度v沿x轴正方向匀速前进,同时以恒定的加速度a由静止匀加速吊起重物(沿y轴正方向),请大致画出重物运动的轨迹.经过t时间,重物的速度大小为$\sqrt{{v^2}+{a^2}{t^2}}$.
如图所示,吊车以恒定速度v沿x轴正方向匀速前进,同时以恒定的加速度a由静止匀加速吊起重物(沿y轴正方向),请大致画出重物运动的轨迹.经过t时间,重物的速度大小为$\sqrt{{v^2}+{a^2}{t^2}}$.
分析 重物参与了水平方向上的匀速直线运动和竖直方向上的匀加速直线运动,通过运动的合成,判断重物相对于地面的运动轨迹以及运动情况.
求出t时刻重物在水平方向和竖直方向上的分速度,根据平行四边形定则,求出重物相对于地面的速度,即合速度.
解答 解:重物在水平方向上做匀速直线运动,在竖直方向上做初速度为0的匀加速直线运动,根据运动的合成,知合速度与合加速度不在同一条直线上,所以重物运动的轨迹为曲线,如图所示: .
.
重物在水平方向上的加速度为0,在竖直方向上有恒定的加速度,根据运动的合成,知猴子做曲线运动的加速度不变,做匀变速曲线运动;
t时刻重物在水平方向上的速度为v0,和竖直方向上的分速度为 vy=at;所以合速度v=$\sqrt{{v^2}+{a^2}{t^2}}$.
故答案为:如上图所示,$\sqrt{{v^2}+{a^2}{t^2}}$.
点评 解决本题的关键知道重物参与了水平方向上的匀速直线运动和竖直方向上的匀加速直线运动,会运用运动的合成分析物体的运动轨迹和运动情况.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
6.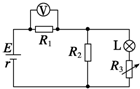 如图所示,R1、R2为定值电阻,L为小灯泡,R3为光敏电阻,当照射光强度增大时电压表的示数增大,下列说法不正确的是( )
如图所示,R1、R2为定值电阻,L为小灯泡,R3为光敏电阻,当照射光强度增大时电压表的示数增大,下列说法不正确的是( )
 如图所示,R1、R2为定值电阻,L为小灯泡,R3为光敏电阻,当照射光强度增大时电压表的示数增大,下列说法不正确的是( )
如图所示,R1、R2为定值电阻,L为小灯泡,R3为光敏电阻,当照射光强度增大时电压表的示数增大,下列说法不正确的是( )| A. | 电压表的示数增大,表明光敏电阻具有随光照增强阻值要增大的特性 | |
| B. | R2中电流减小 | |
| C. | 小灯泡的功率增大 | |
| D. | 电路的路端电压增大 |
4.下列说法正确的是( )
| A. | 根据玻尔理论,氢原子在辐射光子的同时,轨道半径也在连续地减小 | |
| B. | 根据玻尔理论,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增大,电势能减小 | |
| C. | 同一元素的两种同位素具有相同的质子数 | |
| D. | 某放射性原子核经过3次α衰变和一次β衰变,核内质子数减少3个 |
11. 如图所示,质量为1kg的物体静止在光滑水平面上,在与水平成37°角的拉力F=10N作用下运动了2s后,速度变为16m/s,下列说法正确的是( )
如图所示,质量为1kg的物体静止在光滑水平面上,在与水平成37°角的拉力F=10N作用下运动了2s后,速度变为16m/s,下列说法正确的是( )
 如图所示,质量为1kg的物体静止在光滑水平面上,在与水平成37°角的拉力F=10N作用下运动了2s后,速度变为16m/s,下列说法正确的是( )
如图所示,质量为1kg的物体静止在光滑水平面上,在与水平成37°角的拉力F=10N作用下运动了2s后,速度变为16m/s,下列说法正确的是( )| A. | 拉力F在2s末的瞬时功率为128w | B. | 拉力F在2s末的瞬时功率为160w | ||
| C. | 拉力F在2s内的平均功率为80w | D. | 拉力F在2s内的平均功率为160w |
1.某发电厂原来用11kV的交流电压输电,后来改用升压变压器将电压升高到220kV输电,输送的电功率都是P,若输电线路的电阻为R,则下列说法中正确的是( )
| A. | 据公式I=$\frac{P}{U}$,提高电压后输电线上的电流降为原来的$\frac{1}{20}$ | |
| B. | 据公式I=$\frac{U}{R}$,提高电压后输电线上的电流增为原来的20倍 | |
| C. | 据公式P=I2R,提高电压后输电线上的功率损耗减为原来的$\frac{1}{400}$ | |
| D. | 据公式P=$\frac{{U}^{2}}{R}$,提高电压后输电线上的功率损耗将增大为原来400倍 |
8.健身球是现在非常流行的健身保健器具之一,它有很好的弹性,已知某健身球的重力为G0.使用健身球的人重力为G,当人从球的正上方由静止开始压上健身球后(全身离地),下列说法正确的是( )
| A. | 地面对健身球的支持力总是等于G0+G | |
| B. | 健身球对该人的支持力总是等于G | |
| C. | 健身球被压到最扁过程中地面对球的支持力逐渐增大 | |
| D. | 该人在健身球上下降的原因是压健身球的力大于健身球对人的支持力 |
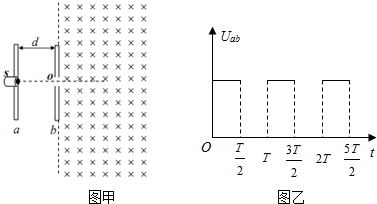
 如图1所示,一个圆形线圈的匝数n=1000,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图2所示;求:
如图1所示,一个圆形线圈的匝数n=1000,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图2所示;求: 在如图所示的电路中,电源的电动势E=28V,内阻r=2Ω,电阻R1=12Ω,R2=R4=4Ω,R3=8Ω,C为平行板电容器,其电容C=3.0pF,虚线到两极板的距离相等,极板长L=0.20m,两极板的间距d=1.0×l0-2m,g取10m/s2.
在如图所示的电路中,电源的电动势E=28V,内阻r=2Ω,电阻R1=12Ω,R2=R4=4Ω,R3=8Ω,C为平行板电容器,其电容C=3.0pF,虚线到两极板的距离相等,极板长L=0.20m,两极板的间距d=1.0×l0-2m,g取10m/s2.