题目内容
7. 如图1所示,一个圆形线圈的匝数n=1000,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图2所示;求:
如图1所示,一个圆形线圈的匝数n=1000,线圈面积S=0.02m2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图2所示;求:(1)前4s内的感应电动势的大小和电流的方向;
(2)在4-6s内通过线圈的电荷量q;
(3)在0-6秒内线圈产生的焦耳热Q.
分析 (1)由法拉第电磁感应定律可以求出感应电动势,由楞次定律可以判断出感应电流的方向.
(2)由法拉第电磁感应定律求出感应电动势,由欧姆定律求出感应电流,由电流的定义式求出电荷量.
(3)应用焦耳定律可以求出线圈产生的焦耳热.
解答 解:(1)由法拉第电磁感应定律可知,前4s内感应电动势:
E1=n$\frac{△Φ}{△t}$=n$\frac{△B}{△t}$S=1000×$\frac{0.4-0.2}{4}$×0.02=1V,
由楞次定律可知,前4室内感应电流沿:逆时针方向;
(2)由法拉第电磁感应定律可知,前4-6s内感应电动势:
E2=n$\frac{△Φ}{△t}$=n$\frac{△B}{△t}$S=1000×$\frac{0.4-0}{6-4}$×0.02=4V,
感应电流:I2=$\frac{{E}_{2}}{r+R}$=$\frac{4}{1+4}$=0.8A,
通过线圈的电荷量:q=I2△t=0.8×2=1.6C;
(3)电流:I1=$\frac{{E}_{1}}{r+R}$=$\frac{1}{1+4}$=0.2A,I2=$\frac{{E}_{2}}{r+R}$=$\frac{4}{1+4}$=0.8A,
线圈产生的热量:Q=Q1+Q2=I12Rt1+I22Rt2=0.22×1×4+0.82×1×2=1.44J;
答:(1)前4s内的感应电动势的大小为1V,电流的方向:逆时针方向;
(2)在4-6s内通过线圈的电荷量q为1.6C;
(3)在0-6秒内线圈产生的焦耳热Q为1.44J.
点评 本题考查了法拉第电磁感应定律的应用,由法拉第电磁感应定律求出感应电动势,由欧姆定律求出感应电流,最后由电流定义式的变形公式求出感应电荷量、由焦耳定律求出焦耳热.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
17.如图所示的a、b、c、d中,质量为M的物体甲受到相同的恒力F的作用,在力F作用下使物体甲在水平方向移动相同的位移.μ表示物体甲与水平面间的动摩擦因数,乙是随物体甲一起运动的小物块,比较物体甲移动的过程中力F对甲所做的功的大小( )


| A. | Wa最小 | B. | Wd最大 | C. | Wa=Wc | D. | 四种情况一样大 |
18.如图是氧气分子在0℃和100℃下的速率分布图线,由图可知( )


| A. | 随着温度升高,氧气分子的平均速率变大 | |
| B. | 随着温度升高,每一个氧气分子的速率都增大 | |
| C. | 随着温度升高,氧气分子中速率小的分子所占比例增大 | |
| D. | 同一温度下,氧气分子速率分布呈现“中间多,两头少”的规律 |
15.如图所示是行星m绕恒星M运动情况的示意图,则下列说法正确的是( )


| A. | 速度最大是在B点 | B. | 速度最大是在A点 | ||
| C. | m从A到B做减速运动 | D. | m从B到A做减速运动 |
12.质量为2kg的物体做自由落体运动,经过2s落地.取g=10m/s2.关于重力做功的功率,下列说法正确的是( )
| A. | 下落过程中重力的平均功率是200W | B. | 第2s内重力的平均功率是300W | ||
| C. | 落地前瞬间重力的瞬时功率是200W | D. | 1s末重力的瞬时功率是200W |
19. 若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )
若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )
 若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )
若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )| A. | O-r0这个区域的电场强度最大 | |
| B. | A点的电场强度可能等于B点的电场强度 | |
| C. | 若r2-r1=r1-r0,则φA-φB=φ0-φA | |
| D. | 将α粒子从A点移到B点,电场力做正功 |
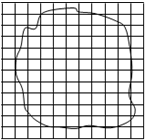 在“用油膜法估测分子的大小”的实验中,油酸酒精溶液的浓度为每104 mL溶液中有纯油酸5mL.用注射器测得1mL上述溶液有液滴100滴.把1滴该溶液滴入盛水的浅盘里,待稳定后,将玻璃板放在浅盘上描出油膜轮廓,再将玻璃板放在坐标纸上,其形状如图所示,坐标纸中正方形小方格的边长为1cm.则:
在“用油膜法估测分子的大小”的实验中,油酸酒精溶液的浓度为每104 mL溶液中有纯油酸5mL.用注射器测得1mL上述溶液有液滴100滴.把1滴该溶液滴入盛水的浅盘里,待稳定后,将玻璃板放在浅盘上描出油膜轮廓,再将玻璃板放在坐标纸上,其形状如图所示,坐标纸中正方形小方格的边长为1cm.则: 一棱镜的截面为直角三角形ABC,∠A=30°,斜边AB=a.棱镜材料的折射率为n=$\sqrt{2}$.在此截面所在的平面内,一条光线从AC边的中点M射入棱镜,方向如图所示,入射角为45°.(不考虑光线沿原路返回的情况)
一棱镜的截面为直角三角形ABC,∠A=30°,斜边AB=a.棱镜材料的折射率为n=$\sqrt{2}$.在此截面所在的平面内,一条光线从AC边的中点M射入棱镜,方向如图所示,入射角为45°.(不考虑光线沿原路返回的情况) 如图所示,吊车以恒定速度v沿x轴正方向匀速前进,同时以恒定的加速度a由静止匀加速吊起重物(沿y轴正方向),请大致画出重物运动的轨迹.经过t时间,重物的速度大小为$\sqrt{{v^2}+{a^2}{t^2}}$.
如图所示,吊车以恒定速度v沿x轴正方向匀速前进,同时以恒定的加速度a由静止匀加速吊起重物(沿y轴正方向),请大致画出重物运动的轨迹.经过t时间,重物的速度大小为$\sqrt{{v^2}+{a^2}{t^2}}$.