题目内容
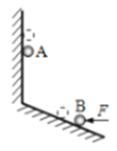
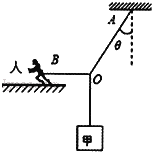
【题目】如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O,轻绳OB水平且B端与站在水平面上的质量为m2的人相连,轻绳OA与竖直方向的夹角![]() 物体甲及人均处于静止状态。(已知
物体甲及人均处于静止状态。(已知![]() ,g取
,g取![]() 。设最大静摩擦力等于滑动摩擦力)求:
。设最大静摩擦力等于滑动摩擦力)求:
(1)轻绳OA、OB受到的拉力分别是多大?
(2)人受到的摩擦力是多大?方向如何?
(3)若人的质量![]() ,人与水平面之间的动摩擦因数为
,人与水平面之间的动摩擦因数为![]() ,欲使人在水平面上不滑动,则物体甲的质量m1最大不能超过多少?
,欲使人在水平面上不滑动,则物体甲的质量m1最大不能超过多少?
【答案】(1)![]() (2)
(2)![]() ,水平向左(3)24kg
,水平向左(3)24kg
【解析】
(1)以结点O为研究对象,分析受力,作出力图,根据平衡条件求出轻绳OA、OB受到的拉力。
(2)人水平方向受到OB绳的拉力和水平面的静摩擦力,由二力平衡求解人受到的摩擦力大小和方向。
(3)当人刚要滑动时,物体甲的质量m1达到最大,此时人受到的静摩擦力达到最大值Fmax=μm2g,再由平衡条件求出物体甲的最大质量。
(1)对结点O进行受力分析,受甲通过绳子对O的拉力m1g,OB的拉力F和OA的拉力T,处于平衡状态,如图所示:![]() ;
;![]()
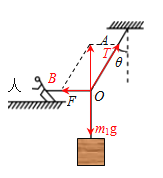
(2)对人受力分析,在水平方向上受OB的拉力F′和地面对人的摩擦力f处于平衡状态,
所以有:![]()
人有向右的运动趋势,所以人受到水平向左的摩擦力作用。
(3)人在竖直方向上受重力m2g和支持力N,若人的质量m2=60kg,人与水平面之间的动摩擦因数μ=0.3,则人受到的最大静摩擦力为:
fmax=μN=μm2g…②
此时物体甲的质量达到最大,联立①②并代入数据得:m1=24kg

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目