题目内容
如图所示,两平行金属板AB中间有互相垂直的匀强电场和匀强磁场。A板带正电荷,B板带等量负电荷,板间电场强度为E;磁场方向垂直纸面向里,磁感应强度为B1。平行金属板右侧有一挡板M,中间有小孔O′,OO′是平行于两金属板的中心线。挡板右侧有垂直纸面向外的匀强磁场,磁场应强度为B2。CD为磁场B2边界上的一绝缘板,它与M板的夹角θ=45°,O′C=a,现有大量质量均为m,含有不同电荷量、不同速度的正、负带电粒子(不计重力),自O点沿OO′方向进入电磁场区域,其中有些粒子沿直线OO′方向运动,并进入匀强磁场B2中,求: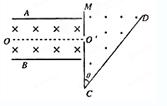
(1)进入匀强磁场B2的带电粒子的速度
(2)能击中绝缘板CD的粒子中,所带电荷量的最大值
(3)绝缘板CD上被带电粒子击中区域的长度
(1) (2)
(2) (3)2a
(3)2a
解析试题分析:(1)设沿直线OO′运动的带电粒子进入匀强磁场B2的速度为
根据:
解得: 。
。
(2)粒子进入匀强磁场B2中做匀速圆周运动
根据:  ,解得:
,解得:
因此电荷量最大的粒子运动的轨道半径最小,设最小半径为r1
由几何关系有: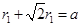 ,解得最大电荷量为:
,解得最大电荷量为:  。
。
(3)带负电的粒子在磁场B2中向上偏转,某带负电粒子轨迹与CD相切,设半径为r2,依题意:
解得: 
则CD板上被带电粒子击中区域的长度为:
考点:本题考查带电粒子在复合场运动(速度选择器)、磁场中的偏转与讨论。

练习册系列答案
相关题目
如图所示,用同种电阻丝制成的正方形闭合线框1的边长与圆形闭合线框2的直径相等.m和n是1线框下边的两个端点,p和q是2线框水平直径的两个端点.1和2线框同时由静止开始释放并进入上边界水平、足够大的匀强磁场中,进入过程中m、n和p、q连线始终保持水平.当两线框完全进入磁场以后,下面说法正确的是
| A.m、n和p、q电势的关系一定有Um<Un,Up<Uq |
| B.m、n和p、q间电势差的关系一定有Umn=Upq |
| C.进入磁场过程中流过1和2线框的电荷量Q1>Q2 |
| D.进入磁场过程中流过1和2线框的电荷量Q1=Q2 |

 、
、 象限内存在方向向里的匀强磁场,磁感应强度大小B=0.5T,处于坐标原点O的放射源不断地放射出比荷
象限内存在方向向里的匀强磁场,磁感应强度大小B=0.5T,处于坐标原点O的放射源不断地放射出比荷 C/kg的正离子,不计离子之间的相互作用。
C/kg的正离子,不计离子之间的相互作用。
 s时间这些离子所在位置构成的曲线方程;
s时间这些离子所在位置构成的曲线方程;


 匀速移动,当与粒子相遇时粒子运动方向恰好与挡板平行,求
匀速移动,当与粒子相遇时粒子运动方向恰好与挡板平行,求 的正电荷置于电场中O点由静止释放,经过
的正电荷置于电场中O点由静止释放,经过 后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
 时刻电荷与O点的竖直距离r。
时刻电荷与O点的竖直距离r。