题目内容
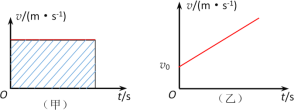
【题目】在匀速直线运动中，物体运动的速度不变，因此位移x=vt，这在数值上恰好等于v-t图像中阴影部分的面积，如图（甲）所示。证明：在初速度为v0、加速度为a的匀变速度直线运动中，如图（乙），梯形的面积在数值上等于匀变速直线运动的位移大小；并推导出位移公式（用v0、a、t表示）。
【答案】见解析
【解析】
在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内就可以近似地应用匀速直线运动的公式来计算位移，如图（甲）所示；如果我们把每一小段
内的运动看做匀速运动，则矩形面积之和等于各段匀速直线运动的位移之和，显然小于匀变速直线运动在该时间内的位移，但所取时间段越小，各匀速直线运动位移之和与匀变速直线运动位移之间的差值就越小，如图（乙）所示，当
时，各矩形面积之和趋近于
图线下面的面积，可以想象，如果把整个运动过程划分得非常细，很多小矩形的面积之和就能准确代表物体的位移了，位移的大小就等于图（丙）所示的梯形面积。
对于匀变速直线运动，运用“无限分割，逐步逼近”的微分思想可得：匀变速直线运动，物体的位移对应图线和时间轴所包围的图像的“面积”。
在图中图线和时间轴所包围的图像的“面积”为
与之对应的物体的位移为
又
联立解得
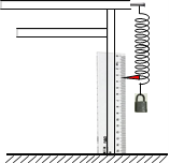
阅读快车系列答案
【题目】某同学在实验室做“探究弹簧弹力的大小与伸长量的关系”实验时，将弹簧悬挂在铁架台上，将刻度尺竖直固定在弹簧一侧，刻度尺的零刻度线刚好与弹簧上端相齐，读出此时弹簧的长度
=25.35cm。在弹簧下端悬挂1个钩码时，弹簧的长度为L1；每次增加1个钩码，分别读出弹簧长度为L2、L3……。已知单个钩码的质量为m=50g，重力加速度g=9.8N/kg。
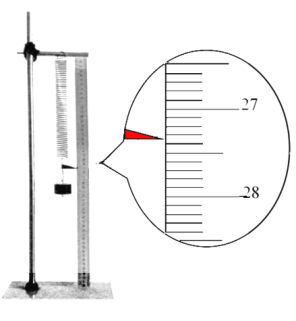
(1)L1的读数如图所示，将L1的数值填入下表__________。
代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
数值/cm | 25.35 |
| 29.35 | 31.30 | 33.40 | 35.35 | 37.40 | 39.35 |
(2)该同学根据表中的数据做出m-L图像，如图所示。其中图像横轴代表弹簧的长度，纵轴代表所悬挂钩码的质量。除第2组数据外，其它数据已在坐标系中描绘出对应点。请将第2组数据的对应点标记在相应位置，并绘出m-L图像__________。
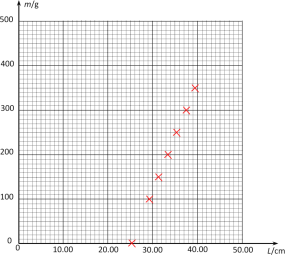
(3)由图像可知，该弹簧的劲度系数k=__________N/m（结果保留两位小数）。
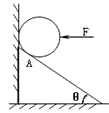
(4)另一同学在家测弹簧的劲度系数。他将弹簧挂在桌子的边缘，如图所示，找到了质量为m的3个同样的铁锁和一把刻度尺，实验时，他将刻度尺竖直立在桌腿边缘靠近弹簧的位置。当挂1个铁锁时，弹簧的指针指在l1位置；当挂3个铁锁时，弹簧的指针指在l2位置。重力加速度为g。由此可得该弹簧的劲度系数k=________（用l1、l2、m、g表示）。
