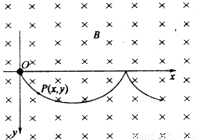
题目内容
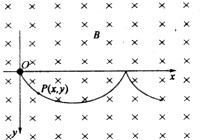
在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O点静止释放,小球的运动曲线如图所示。已知此曲线在最低点的曲率半径为该点到x轴距离的2倍,重力加速度为g。求:
(1)小球运动到任意位置P(x,y)处的速率v;
(2)小球在运动过程中第一次下降的最大距离ym;
(3)当在上述磁场中加一竖直向上场强为E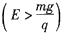 的匀强电场时,小球从O点静止释放后获得的最大速率vm。
的匀强电场时,小球从O点静止释放后获得的最大速率vm。
(1)小球运动到任意位置P(x,y)处的速率v;
(2)小球在运动过程中第一次下降的最大距离ym;
(3)当在上述磁场中加一竖直向上场强为E
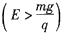 的匀强电场时,小球从O点静止释放后获得的最大速率vm。
的匀强电场时,小球从O点静止释放后获得的最大速率vm。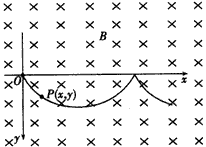
解:(1)洛伦兹力不做功,由动能定理得
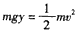 ①
①
得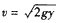 ②
②
(2)设在最大距离ym处的速度为vm,根据圆周运动有
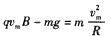 ③
③
且由②知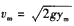 ③
③
由③④及R=2ym得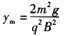 ⑤
⑤
(3)小球运动如图所示
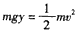 ①
①得
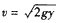 ②
② (2)设在最大距离ym处的速度为vm,根据圆周运动有
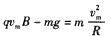 ③
③且由②知
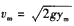 ③
③ 由③④及R=2ym得
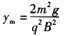 ⑤
⑤ (3)小球运动如图所示

由动能定理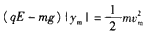 ⑥
⑥
由圆周运动 ⑦
⑦
且由⑥⑦及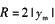 解得
解得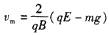
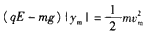 ⑥
⑥ 由圆周运动
 ⑦
⑦且由⑥⑦及
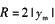 解得
解得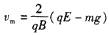

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2008?江苏)(平常练习改变)在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求:
(2008?江苏)(平常练习改变)在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求: (3)当在上述磁场中加一竖直向上场强为E(
(3)当在上述磁场中加一竖直向上场强为E(