题目内容
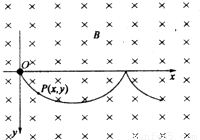
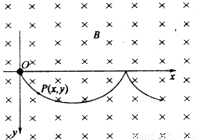
(平常练习改变)在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求:(1)小球运动到任意位置P(x,y)的速率v.
(2)小球在运动过程中第一次下降的最大距离ym.
(3)当在上述磁场中加一竖直向上场强为E(E>mg/q)的匀强电场时,小球从O静止释放后获得的最大速率vm.
【答案】分析:(1)首先分析,在任意时刻,小球都只受到重力和洛伦兹力.洛伦兹力始终方向与速度方向垂直,不做功,所以从原点到最低点只有重力做功,根据动能定理即可求得速度;
(2)设小球在最低点的速度为v,到x轴距离为h,最低点的曲率半径为2h.对于小球运动到最低点时,小球的向心力由洛伦兹力与重力的合力提供,列出向心力公式,再结合第一问中的速度就可以求出小球在运动过程中第一次下降的最大距离ym;
(3)加入电场后,结合动能定理和圆周运动向心力的公式即可以求得小球从O静止释放后获得的最大速率vm.
解答: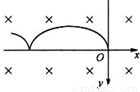 解析:(1)洛仑兹力不做功,由动能定理得,
解析:(1)洛仑兹力不做功,由动能定理得,
mgy= mv2 ①
mv2 ①
得 v=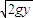 ②
②
(2)设在最大距离ym处的速率为vm,根据圆周运动有,qvmB-mg=m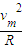 ③
③
且由②知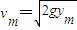 ④
④
由③④及R=2ym得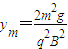 ⑤
⑤
(3)小球运动如图所示,
由动能定理 (qE-mg)|ym|=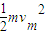 ⑥
⑥
由圆周运动 qvmB+mg-qE=m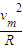 ⑦
⑦
且由⑥⑦及R=2|ym|解得
vm=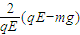 .
.
点评:本题涉及到的知识点有洛伦兹力的性质(无论何时都不做功)、机械能守恒的条件与计算、圆周运动的计算,对同学们分析问题的能力要求较高,属于中档偏上的题目.
(2)设小球在最低点的速度为v,到x轴距离为h,最低点的曲率半径为2h.对于小球运动到最低点时,小球的向心力由洛伦兹力与重力的合力提供,列出向心力公式,再结合第一问中的速度就可以求出小球在运动过程中第一次下降的最大距离ym;
(3)加入电场后,结合动能定理和圆周运动向心力的公式即可以求得小球从O静止释放后获得的最大速率vm.
解答:
 解析:(1)洛仑兹力不做功,由动能定理得,
解析:(1)洛仑兹力不做功,由动能定理得,mgy=
 mv2 ①
mv2 ①得 v=
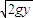 ②
②(2)设在最大距离ym处的速率为vm,根据圆周运动有,qvmB-mg=m
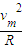 ③
③且由②知
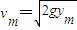 ④
④由③④及R=2ym得
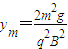 ⑤
⑤(3)小球运动如图所示,
由动能定理 (qE-mg)|ym|=
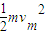 ⑥
⑥由圆周运动 qvmB+mg-qE=m
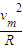 ⑦
⑦且由⑥⑦及R=2|ym|解得
vm=
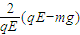 .
.点评:本题涉及到的知识点有洛伦兹力的性质(无论何时都不做功)、机械能守恒的条件与计算、圆周运动的计算,对同学们分析问题的能力要求较高,属于中档偏上的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2007?四川)如图所示,一根长L=1.5m的光滑绝缘细直杆MN,竖直固定在场强为E=1.0×105N/C、与水平方向成θ=30°角的倾斜向上的匀强电场中.杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6C,质量m=1.0×10-2kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109N?m2/C2,取g=l0m/s2)
(2007?四川)如图所示,一根长L=1.5m的光滑绝缘细直杆MN,竖直固定在场强为E=1.0×105N/C、与水平方向成θ=30°角的倾斜向上的匀强电场中.杆的下端M固定一个带电小球A,电荷量Q=+4.5×10-6C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6C,质量m=1.0×10-2kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×109N?m2/C2,取g=l0m/s2) 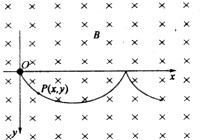 (2008?江苏)(平常练习改变)在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求:
(2008?江苏)(平常练习改变)在场强为B的水平匀强磁场中,一质量为m、带正电q的小球在O静止释放,小球的运动曲线如图所示.已知此曲线在最低点的曲率半径为该点到z轴距离的2倍,重力加速度为g.求: