题目内容
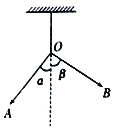
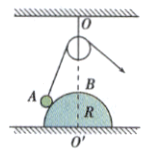
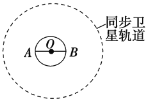
【题目】如图所示,设A、B为地球赤道圆的一条直径的两端点,利用两颗 同步地球卫星作为中继就可以将一电磁波信号由A点传到B点。已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对电磁波的折射.设电磁波在空气中沿直线传播且传播速度为c.求:
(1)这两颗同步卫星间的最小距离s是多少?
(2)同步卫星的轨道半径r是多少?
(3)用这两颗卫星把电磁波信号由A点传到B点需要经历的时间t是多少?
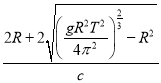
【答案】(1)2R(2)![]() (3)
(3)
【解析】
(1)由图可明显地看出,为实现上述目的,至少需要两颗同步卫星,其位置在P1、P2,如图所示:
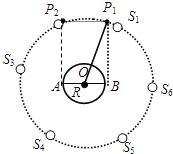
则由图可知这两颗同步卫星的最近距离是2R
(2)设同步卫星的轨道半径为r=OP1,根据万有引力提供向心力,则有:
![]()
在地球表面,不考虑自转,则有:
![]()
联立解得:![]()
(3)由图可见,此时通过这两颗同步卫星由A到B传播电磁波信号经过的路程为:
![]()
根据勾股定理有:
![]()
则这两颗卫星把电磁波信号由A点传到B点需要经历的时间为:
![]()
解得: 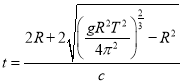

练习册系列答案
相关题目