题目内容
10.氢原子核外电子在第一轨道上运动时,能量E=-13.6eV,轨道半径r1=0.53×10-10m.这时电子运动的动能是多少电子伏?电势能是多少电子伏?分析 根据库仑引力提供电子做圆周运动的向心力,求出电子在轨道上的动能.
原子的能量等于电势能和电子动能之和,从而求出电子具有的电势能.
解答 解:(1)原子核对电子的库仑力提供向心力,由牛顿第二定律及库仑定律得:
$\frac{{ke}^{2}}{{r}_{1}^{2}}$=$\frac{{mv}^{2}}{{r}_{1}}$
电子运动的动能为:Ek=$\frac{1}{2}$mv2=13.6 eV,
(2)原子的能量等于电势能和电子动能之和,即E1=Ek1+EP1
所以电势能 Ep1=E1-Ek1=-27.2eV
答:这时电子运动的动能是13.6eV,电势能是-27.2eV.
点评 解决本题的关键知道原子的能量等于电势能与电子动能之和,会通过库仑引力提供向心力求出电子的动能.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.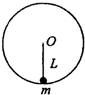 如图所示,长为L的轻杆一端固定一个质量为m的小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕轴O在坚直平面内转动,不计空气阻力,则( )
如图所示,长为L的轻杆一端固定一个质量为m的小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕轴O在坚直平面内转动,不计空气阻力,则( )
 如图所示,长为L的轻杆一端固定一个质量为m的小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕轴O在坚直平面内转动,不计空气阻力,则( )
如图所示,长为L的轻杆一端固定一个质量为m的小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕轴O在坚直平面内转动,不计空气阻力,则( )| A. | 小球到达最高点的速度必须等于$\sqrt{GL}$ | |
| B. | 小球到达最高点的速度可能为0 | |
| C. | 小球到达最高点受杆的作用力一定为拉力 | |
| D. | 小球到达最高点受杆的作用力一定为支持力 |
5.质量为0.2kg的小球做自由落体运动,在其下落过程中,第1s末重力做功的瞬时功率为 ;1s内重力做功的平均功率为 (g取10m/s2)( )
| A. | 10 W;10 W | B. | 15 W;15 W | C. | 20 W;10 W | D. | 25 W;15 W |
2.汽车通过圆形拱桥顶点时对桥的压力为车重的$\frac{1}{2}$,若拱桥的半径为R=20m,则此时汽车的速度为( )
| A. | 10m/s | B. | 20m/s | C. | 25m/s | D. | 30m/s |
19. 用轻质细线把小球悬挂在O点,在O点的正下方有一钉子,把细线沿水平方向拉直,如图所示.无初速度地释放小球,当细线碰到钉子的时刻,则以下说法正确的是( )
用轻质细线把小球悬挂在O点,在O点的正下方有一钉子,把细线沿水平方向拉直,如图所示.无初速度地释放小球,当细线碰到钉子的时刻,则以下说法正确的是( )
 用轻质细线把小球悬挂在O点,在O点的正下方有一钉子,把细线沿水平方向拉直,如图所示.无初速度地释放小球,当细线碰到钉子的时刻,则以下说法正确的是( )
用轻质细线把小球悬挂在O点,在O点的正下方有一钉子,把细线沿水平方向拉直,如图所示.无初速度地释放小球,当细线碰到钉子的时刻,则以下说法正确的是( )| A. | 小球的角速度大小不变 | |
| B. | 小球的线速度大小不变 | |
| C. | 小球的向心加速度大小不变 | |
| D. | 钉子离O点越远,碰钉子时,细线越容易断 |
20.一条小船浮在湖面上静止不动,船长3m,质量140kg,当一个质量为m=70kg的人从船头走到船尾时,人相对于河岸移动了( )
| A. | 3 m | B. | 0 m | C. | 1 m | D. | 2 m |
 长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求:
长度为L细绳,一端系有一质量为m的小球,小球以O点为圆心在竖直面内做圆周运动,求: