题目内容
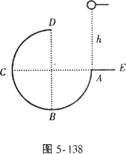
如图所示，AB为固定在竖直平面内的
光滑圆弧轨道，轨道的B点与水平地面相切，其半径为R.质量为m的小球由A点静止释放，求：
（1）小球滑到最低点B时，小球速度v的大小及小球对轨道的压力F压的大小；
（2）小球通过光滑的水平面BC滑上固定曲面，恰达最高点D，D到地面的高度为h（已知h＜R），则小球在曲面上克服摩擦力所做的功Wf.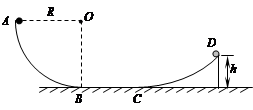
光滑圆弧轨道，轨道的B点与水平地面相切，其半径为R.质量为m的小球由A点静止释放，求：（1）小球滑到最低点B时，小球速度v的大小及小球对轨道的压力F压的大小；
（2）小球通过光滑的水平面BC滑上固定曲面，恰达最高点D，D到地面的高度为h（已知h＜R），则小球在曲面上克服摩擦力所做的功Wf.
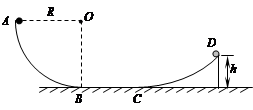
（1） 
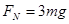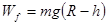
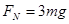（2）
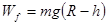
（2） 解：⑴由动能定理得
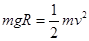，………………………………2分
解得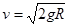
………………………………1分
由牛顿第二定律得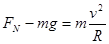
，………………………………2分
解得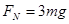………………………………1分
（2）由动能定理得
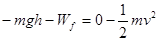………………………………4分
解得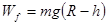……………………2分
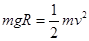，………………………………2分解得
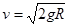………………………………1分由牛顿第二定律得
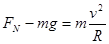，………………………………2分解得
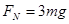………………………………1分（2）由动能定理得
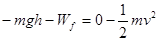………………………………4分解得
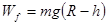……………………2分
练习册系列答案
阅读快车系列答案
相关题目
