题目内容
(2009?天津)2008年12月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的倍数关系.研究发现,有一星体S2绕人马座A*做椭圆运动,其轨道半长轴为9.50×102天文单位(地球公转轨道的半径为一个天文单位),人马座A*就处在该椭圆的一个焦点上.观测得到S2星的运行周期为15.2年.
(1)若将S2星的运行轨道视为半径r=9.50×102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量Ms的多少倍(结果保留一位有效数字);
(2)黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚.由于引力的作用,黑洞表面处质量为m的粒子具有势能为Ep=-G
(设粒子在离黑洞无限远处的势能为零),式中M、R分别表示黑洞的质量和半径.已知引力常量G=6.7×10-11N?m2/kg2,光速c=3.0×108m/s,太阳质量Ms=2.0×1030kg,太阳半径Rs=7.0×108m,不考虑相对论效应,利用上问结果,在经典力学范围内求人马座A*的半径RA与太阳半径Rg之比应小于多少(结果按四舍五入保留整数).
(1)若将S2星的运行轨道视为半径r=9.50×102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量Ms的多少倍(结果保留一位有效数字);
(2)黑洞的第二宇宙速度极大,处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚.由于引力的作用,黑洞表面处质量为m的粒子具有势能为Ep=-G
| Mm | R |
分析:研究S2星绕人马座A*做圆周运动,根据万有引力提供向心力,列出等式求出人马座A*的质量.
研究地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式求出太阳的质量.
根据题目提供的信息,筛选出有用的信息,结合功能关系,求出问题.
研究地球绕太阳做圆周运动,根据万有引力提供向心力,列出等式求出太阳的质量.
根据题目提供的信息,筛选出有用的信息,结合功能关系,求出问题.
解答:解:(1)S2星绕人马座A*做圆周运动的向心力由人马座A*对S2星的万有引力提供,设S2星的质量为mS2,角速度为ω,周期为T,则G
=mS2ω2r ①
ω=
②
设地球质量为mE,公转轨道半径为rE,周期为TE,研究地球绕太阳做圆周运动,根据万有引力提供向心力则
G
=mEω2rE ③
综合上述三式得
=(
)3(
)2
式中 TE=1年,rE=1天文单位,
代入数据可得
=4×106
(2)引力对粒子作用不到的地方即为无限远,此时粒子的势能为零.“处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚”,说明了黑洞表面处以光速运动的粒子在远离黑洞的过程中克服引力做功,粒子在到达无限远之前,其动能便减小为零,此时势能仍为负值,则其能量总和小于零,则有
mc2-G
<0 ④
依题意可知R=RA,M=MA
可得RA<
⑤
代入数据得RA<1.2×1010 m
所以:
<17
答:(1)人马座A*的质量MA是太阳质量Ms的4×106倍,
(2)在经典力学范围内求人马座A*的半径RA与太阳半径Rg之比应小于17.
| MAmS2 |
| r2 |
ω=
| 2π |
| T |
设地球质量为mE,公转轨道半径为rE,周期为TE,研究地球绕太阳做圆周运动,根据万有引力提供向心力则
G
| MSmE | ||
|
综合上述三式得
| MA |
| MS |
| r |
| rE |
| TE |
| T |
式中 TE=1年,rE=1天文单位,
代入数据可得
| MA |
| MS |
(2)引力对粒子作用不到的地方即为无限远,此时粒子的势能为零.“处于黑洞表面的粒子即使以光速运动,其具有的动能也不足以克服黑洞对它的引力束缚”,说明了黑洞表面处以光速运动的粒子在远离黑洞的过程中克服引力做功,粒子在到达无限远之前,其动能便减小为零,此时势能仍为负值,则其能量总和小于零,则有
| 1 |
| 2 |
| Mm |
| R |
依题意可知R=RA,M=MA
可得RA<
| 2GMA |
| c2 |
代入数据得RA<1.2×1010 m
所以:
| RA |
| RS |
答:(1)人马座A*的质量MA是太阳质量Ms的4×106倍,
(2)在经典力学范围内求人马座A*的半径RA与太阳半径Rg之比应小于17.
点评:本题考查天体运动的知识.其中第2小题为信息题,如“黑洞”“引力势能”等陌生的知识都在题目中给出,考查学生提取信息,处理信息的能力,体现了能力立意.
求一个物理量之比,我们可以把这个物理量先用已知的物理量表示出来,再进行之比.
求一个物理量之比,我们可以把这个物理量先用已知的物理量表示出来,再进行之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2009?天津)如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为θ.不计空气阻力,重力加速度为g,求
(2009?天津)如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为θ.不计空气阻力,重力加速度为g,求 (2009?天津)如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求
(2009?天津)如图所示,质量m1=0.3kg 的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求 (2009?天津模拟)核聚变能以氘、氚等为燃料,具有安全、洁净、储量丰富三大优点,是最终解决人类能源危机的最有效手段.
(2009?天津模拟)核聚变能以氘、氚等为燃料,具有安全、洁净、储量丰富三大优点,是最终解决人类能源危机的最有效手段.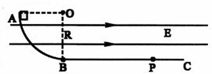 (2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)
(2009?天津模拟)如图所示,竖直面内有一绝缘轨道,AB部分是光滑的四分之一圆弧,圆弧半径R=0.5m,B处切线水平,BC部分为水平粗糙直轨道.有一个带负电的小滑块(可视为质点)从A点由静止开始下滑,运动到直轨道上的P处刚好停住.小滑块的质量m=1kg,带电量为q=-2.5×10-3C保持不变,滑块小轨道BC部分间的动摩擦因数为μ=0.2,整个空间存在水平向右的匀强电场,电场强度大小为E=4.0×102N/C.(g=10m/s2)