题目内容
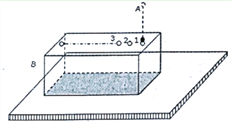
【题目】如图，A为位于一定高度处的质量为m、带电荷量为+q的小球，B为位于水平地面上的质量为M的用特殊材料制成的长方形空心盒子，且M=2m，盒子与地面间的动摩擦因数为
（n取自然数），盒内存在着竖直向上的匀强电场，场强大小
，盒外没有电场。盒子的上表面开有一系列略大于小球的小孔1、2、3.…，孔间距满足一定的关系，使得小球进出盒子的过程中始终不与盒子接触。当小球A以v0的速度从孔1进入盒子的瞬间，盒子B恰以6 v0的速度向右滑行。已知盒子通过电场对小球施加的作用力与小球通过电场对盒子施加的作用力大小相等方向相反。设盒子足够长，小球恰能顺次从各个小孔进出盒子。试求：
（1）小球A从第一次进入盒子到第二次进入盒子所经历的时间；
（2）小球A从第一次进入盒子到第二次进入盒子的过程中，盒子的位移；
（3）小球A从第一次进入盒子至盒子停止运动的过程中，盒子通过的总路程。
【答案】（1）
（2）
（3）
【解析】试题分析：小球A从第一次进入盒子到第二次进入盒子所经历的时间分为两部分，A在盒子内运动时运动牛顿第二定律求出加速度，再用运动学基本公式求出时间，A在盒子外运动的时间根据运动学基本公式即可求得，时间之和即为经历的总时间；分别求出盒子在每个周期内通过的距离，观察数据得特点，通过数学等差数列知识求出盒子通过的总路程。
(1) A在盒子内运动时，有：qE-mg=ma，
由以上两式得：a=g
在盒子内运动的时间为： 
，A在盒子外运动的时间为： 
A从第一次进入盒子到第二次进入盒子的时间为： 
(2) 球在盒子内运动,盒子的加速度
球在盒子外运动时盒子的加速度
小球第一次在盒子内运动的过程中,盒子前进的距离
小球第一次从盒子出来时,盒子的速度
球第一次在盒子外运动时
由以上三式解得： 
；
(3) 小球第一次在盒内运动的过程中，盒子前进的距离为： 
小球第一次从盒子出来时，盒子的速度为： 
小球第一次在盒外运动的过程中，盒子前进的距离为： 
小球第二次进入盒子时，盒子的速度为： 
小球第二次在盒子内运动的过程中，盒子前进的距离为： 
小球第二次从盒子出来时，盒子的速度
小球第二次在盒外运动的过程中，盒子前进的距离为： 
分析上述各组数据可知，盒子在每个周期内通过的距离为一等差数列，公差
项数是2n项，最后一项是： 
所以总路程为： 
。
点晴：该题是较为复杂的往复运动，要求同学们能正确分析每个过程的受力情况，求出加速度、时间和位移，还要善于观察数据，总结数据之间的规律，要求较高，难度很大，属于难题。
