题目内容
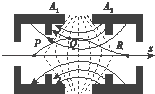
【题目】如图所示，传送带A、B之间的距离为L＝3.2 m，与水平面间的夹角θ＝37°，传送带沿顺时针方向转动，速度恒为v＝2 m/s，在上端A点无初速度地放置一个质量为m＝1 kg、大小可视为质点的金属块，它与传送带的动摩擦因数为μ＝0.5，金属块滑离传送带后，经过弯道，沿半径为R＝0.4 m的光滑圆轨道做圆周运动，刚好能通过最高点E。已知B、D两点的竖直高度差h＝0.6 m(g取10 m/s2)求：
(1)金属块经过D点时的速度；
(2)金属块在BCD弯道上克服摩擦力做的功。
【答案】（1）
（2）4 J
【解析】试题分析：（1）金属块刚好能通过最高点E，对金属块在E点，有：mg=m
代入数据解得：v=2m/s （2分）
在从D到E过程中，由动能定理得：
代入数据得：
； （3分）
（2）金属块刚刚放上时，对金属块受力分析，在沿传送带方向的加速度为a1，
沿传送带建立坐标有：mgsinθ+μmgcosθ=ma1
代入数据得：a1=10m/s2 （2分）
设经位移s1达到共同速度，由运动学公式有：v2=2as1
代入数据解得：s1=0．2＜3．2m； 可知物体并未到达传送带底端，所以将继续加速 （2分）
继续加速过程中，有：mgsinθ﹣μmgcosθ=ma2
代入数据解得：a2=2m/s2 （1分）
再次加速过程中的位移为：s2=L﹣s1=3m 令到达B端时的速度为vB，
由运动学公式有：vB2﹣v2=2a2s2代入数据解得：vB=4m/s （2分）
在从B到D过程中，重力做正功、摩擦力做负功为W。由动能定理可知：
解得：W=3J； （2分）
练习册系列答案
相关题目
