题目内容
如图所示，在一真空区域中，AB、CD是圆O的两条直径，在A、B两点上各放置电荷量为+Q和-Q的点电荷，设C、D两点的电场强度分别为EC、ED，电势分别为φC、φD，则EC与ED （选填“相同”或“不相同”），φC与φD （选填“相等”或“不相等”）．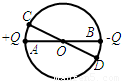
【答案】分析：可以将一个带正点的试探电荷+q分别放在C、D两点，通过矢量合成确定其受到的电场力的合力方向和大小进行判断，也可以结合带等量异号电荷的电场的电场线进行判断；对于电势，可以根据沿着电场线电势减小和电场的对称性进行判断．
解答：解：带等量异号电荷的电场的电场线如图
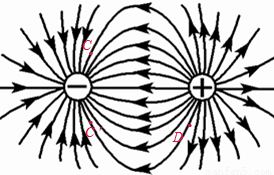
可以看出C、D两点的电场强度大小相等、方向相同；
沿着电场线电势减小，D点电势一定大于C′点电势，而C点电势等于C点电势，故D点电势一定大于C点电势；
故答案为：相同，不相等．
点评：本题关键是结合等量异号电荷的电场线图线进行分析处理，要明确沿着电场线，电势逐渐降低，电场线的疏密程度表示电场强度的大小，电场线上任意一点的切线方向表示该点的电场强度方向．
解答：解：带等量异号电荷的电场的电场线如图
可以看出C、D两点的电场强度大小相等、方向相同；
沿着电场线电势减小，D点电势一定大于C′点电势，而C点电势等于C点电势，故D点电势一定大于C点电势；
故答案为：相同，不相等．
点评：本题关键是结合等量异号电荷的电场线图线进行分析处理，要明确沿着电场线，电势逐渐降低，电场线的疏密程度表示电场强度的大小，电场线上任意一点的切线方向表示该点的电场强度方向．
练习册系列答案
阅读快车系列答案
相关题目
（2007?苏州二模）处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光，称为氢光谱．氢光谱线的波长可以用下面的巴耳末-里德伯公式
[物理--选修3-4]
一种测定电子比荷的实验装置如图所示．真空玻璃管内，阴极K发出的电子经阳极A与阴极K之间的高压加速后，形成一细束电子流，以平行于平板电容器极板的速度进入两极板C、D间的区域，若两极板C、D间无电压，电子将打在荧光屏上的O点，若在两极板间施加电压U，则离开极板区域的电子将打在荧光屏上的P点；若再在极板间施加一个方向垂直于纸面向外、磁感应强度为B的匀强磁场，则电子在荧光屏上产生的光点又回到O．已知极板的长度l=25cm．C、D间的距离d=5cm，极板区的中点M到荧光屏中点O的距离为 L=25cm，U=128V，B=1.6×10-4T．P点到O点的距离y=10cm，试求电子的比荷．
，如果增大双缝到光屏之间的距离，
，不考虑光的干涉和衍射，试问：
，请你求出圆形亮区的半径。