题目内容
【题目】如图所示，AB是倾角为θ=30°的粗糙直轨道，BCD是光滑的圆弧轨道，AB恰好在B点与圆弧相切，圆弧的半径为R，一个质量为m的物体(可以看做质点)从直轨道上的P点由静止释放，结果它能在两轨道间做往返运上动。已知P点与圆弧的圆心O等高，物体与轨道AB间的动摩擦因数为μ。求：
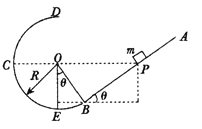
(1)物体做往返运动的整个过程中在AB轨道上通过的总路程；
(2)最终当物体通过圆弧轨道最低点E时，对圆弧轨道的压力；
(3)释放点距B点的距离L′至少多大，物体能顺利到达圆弧轨道的最高点D。
【答案】（1）
；（2）
；（3）
【解析】
（1）物体从P点出发至最终到达B点速度为零的全过程，由动能定理得
mgRcosθ—μmgcosθ=0
所以:
（2）最终物体以B（还有B关于OE的对称点）为最高点，在圆弧底部做往复运动，物体从B运动到E的过程，由动能定理得:
在E点，由牛顿第二定律得：
联立解得：
则物体对圆弧轨道的压力:
（3）L=(3+2cosθ)R/2（sinθ-μcosθ）
练习册系列答案
相关题目
