题目内容
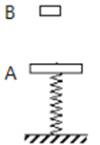
【题目】如图所示,一轻弹簧竖直放置在地面上,下端固定,上端连接一质量为 1kg 的物体A,A处于静止状态,此时弹簧被压缩了0.15m。质量也为 1kg 的物体B从A正上方 h =0.2m 处自由下落,然后A、B结合在一起向下运动。设弹簧形变量为x时的弹性势能为Ek=kx2/2,其中k为弹簧的劲度系数。不计空气阻力, 重力加速度 g=10m/s 2。
求
①碰撞后瞬间两物体的总动能
②碰后AB的最大动能。
【答案】① 1J ②1.75J
【解析】
试题分析:(1)A、B的质量相等,设为m.物体B自由下落时,由机械能守恒定律得:
mgh=![]() mv02
mv02
解得:![]() ;
;
碰撞过程A、B的动量守恒,以向下为正方向,由动量守恒定律得:
mv0=(m+m)v
代入数据解得:![]() ;
;
碰后A、B的总动能:EK=![]() (m+m)v2
(m+m)v2
代入数据解得:EK=1.5J;
(2)A处于静止状态时,由胡克定律得 mg=kx1,得![]()
碰后A、B一起向下运动,弹簧的弹力不断增大,当弹力与AB的总重力大小相等时,动能最大.设此时弹簧的压缩量为x2.则有 2mg=kx2;
可得 x2=2x1=0.3m
从碰后到动能最大的过程中A、B下降的高度为 h′=x2-x1=0.15m
根据系统的机械能守恒得:
![]()
解得碰后A、B的最大动能 EKm=0.75J;

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目