题目内容
1. 如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求:
如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求:(1)A点与O点的竖直高度;
(2)运动员离开O点时的速度大小.
分析 根据时间,结合位移时间公式求出A点与O点的竖直高度.根据水平位移和时间求出运动员离开O点的速度大小.
解答 解:(1)A点与O点的竖直高度为:h=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×9m=45m$.
(2)根据$tan37°=\frac{h}{x}$,则水平位移为:x=$\frac{h}{tan37°}=\frac{45}{\frac{3}{4}}m=60m$,
可知运动员离开O点的速度大小为:v=$\frac{x}{t}=\frac{60}{3}m/s=20m/s$.
答:(1)A点与O点的竖直高度为45m;
(2)运动员离开O点时的速度大小为20m/s.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
相关题目
11.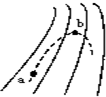 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )| A. | 电荷从a到b加速度减小 | B. | b处电势能比a处电势能小 | ||
| C. | b处电势比a处电势高 | D. | 电荷在b处速度达到最小 |
 如图所示,轻绳OA的A端系一光滑的轻质小环,用力F(未知)拉同时跨过小环和滑轮B的轻绳使物体P在竖直面上向上作匀加速直线运动.P的加速度为a,在此期间位于水平台上与轻绳OA相连的物体Q一直处于静止.已知P的质量为m,力F的方向保持不变,绳OA始终处于水平,A、B连线与竖直方向的夹角为θ=30°,不计滑轮的质量和摩擦,绳不可伸长且有足够长度,重力加速度为g,求Q所受到的摩擦力大小.
如图所示,轻绳OA的A端系一光滑的轻质小环,用力F(未知)拉同时跨过小环和滑轮B的轻绳使物体P在竖直面上向上作匀加速直线运动.P的加速度为a,在此期间位于水平台上与轻绳OA相连的物体Q一直处于静止.已知P的质量为m,力F的方向保持不变,绳OA始终处于水平,A、B连线与竖直方向的夹角为θ=30°,不计滑轮的质量和摩擦,绳不可伸长且有足够长度,重力加速度为g,求Q所受到的摩擦力大小. 如图所示,在x轴下方存在着正交的匀强电场与匀强磁场,电场方向沿x轴正方向,电场强度的大小E1=20N/C,磁场方向垂直纸面向里,磁感应强度的大小B1=5T,一个质量为3g,电荷量q=2×10-3C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点,且已知OM=4m,在x轴上方存在着正交的匀强电场E2与匀强磁场B2(图中均未画出),小球在x轴上方作匀速圆周运动,运动轨迹恰好与y轴相切,如图所示,试求:(g=10m/s2,sin37°=0.6,cos37°=0.8).
如图所示,在x轴下方存在着正交的匀强电场与匀强磁场,电场方向沿x轴正方向,电场强度的大小E1=20N/C,磁场方向垂直纸面向里,磁感应强度的大小B1=5T,一个质量为3g,电荷量q=2×10-3C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点,且已知OM=4m,在x轴上方存在着正交的匀强电场E2与匀强磁场B2(图中均未画出),小球在x轴上方作匀速圆周运动,运动轨迹恰好与y轴相切,如图所示,试求:(g=10m/s2,sin37°=0.6,cos37°=0.8). 在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求小球做匀速圆周运动时,
在如图所示的圆锥摆中,已知绳子长度为L,绳子转动过程中与竖直方向的夹角为θ,求小球做匀速圆周运动时, 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1.0m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.20kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1.0m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.20kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.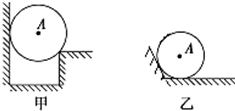
 如图所示,是一列简谐横波在某一时刻的波形图象,已知该波沿x轴正方向传播,波速为5m/s,求:
如图所示,是一列简谐横波在某一时刻的波形图象,已知该波沿x轴正方向传播,波速为5m/s,求: