题目内容
16. 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1.0m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.20kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1.0m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.20kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8.0W,求该速度的大小;
(3)在上问中,若R=2.0Ω,金属棒中的电流方向由a到b,求磁感应强度的大小和方向.(g=10m/s2,sin37°=0.60,cos37°=0.80)
分析 (1)开始下滑时,速度为零,无感应电流产生,因此不受安培力,故根据牛顿第二定律可直接求解结果.
(2)金属棒下滑速度达到稳定时,金属棒所受合外力为零,根据平衡条件求出安培力,然后根据公式P=Fv求解.
(3)结合第(2)问求出回路中的感应电流,然后根据电功率的公式求解.
解答 解:(1)金属棒开始下滑的初速为零,根据牛顿第二定律:mgsinθ-μmgcosθ=ma ①
由①式解得a=10×(O.6-0.25×0.8)m/s2=4m/s2 ②
故金属棒沿导轨由静止开始下滑时的加速度大小为4m/s2.
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡
mgsinθ一μmgcosθ一F=0 ③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率:P=Fv ④
由③、④两式解得$v=\frac{P}{F}=\frac{8}{0.2×10×(0.6-0.25×0.8)}m/s=10m/s$ ⑤
故当金属棒下滑速度达到稳定时,棒的速度大小为10m/s.
(3)设电路中电流为I,两导轨间金属棒的长为l,磁场的磁感应强度为B $I=\frac{vBl}{R}$⑥
P=I2R ⑦
由⑥、⑦两式解得:$B=\frac{{\sqrt{PR}}}{vl}=\frac{{\sqrt{8×2}}}{10×1}T=0.4T$⑧
磁场方向垂直导轨平面向上.
故磁感应强度的大小为0.4T,方向垂直导轨平面向上.
答:(1)金属棒沿导轨由静止开始下滑时的加速度大小为4m/s2;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8.0W,该速度的大小为10m/s;
(3)在上问中,若R=2.0Ω,金属棒中的电流方向由a到b,磁感应强度的大小为0.4T;方向垂直于斜面向上.
点评 本题考查导体切割磁感线的功能关系及受力分析问题,此类问题的突破口为正确分析安培力的变化,根据运动状态列方程求解.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 如图所示,理想变压器的输入端接正弦交变电流,副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,开关S断开.当S接通时,以下说法中正确的是( )
如图所示,理想变压器的输入端接正弦交变电流,副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,开关S断开.当S接通时,以下说法中正确的是( )| A. | 副线圈的两端M、N的输出电压减小 | |
| B. | 副线圈输电线等效电阻R上的电压增大 | |
| C. | 通过灯泡L1的电流减小 | |
| D. | 原线圈中的电流增大 |
| A. | 伽利略通过“理想实验”得出“力是维持物体运动的原因” | |
| B. | 楞次发现了电流的磁效应,拉开了研究电与磁相互关系的序幕 | |
| C. | 法拉第发现了通电导线的周围存在磁场 | |
| D. | 胡克认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 |
| A. | 研究瓢虫身上的星数 | B. | 研究瓢虫翅膀振动情况 | ||
| C. | 研究瓢虫飞行路线 | D. | 研究瓢虫如何起飞和停落 |
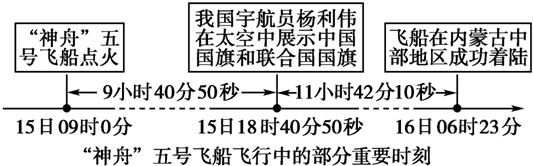
| A. | “神舟”五号飞船点火的时刻是15日09时0分 | |
| B. | “神舟”五号飞船从点火到杨利伟在太空中展示中国国旗和联合国国旗用的时间是9小时40分50秒 | |
| C. | 飞船成功着陆的时间是11小时42分10秒 | |
| D. | “神舟”五号飞船在空中总飞行时间为21小时23分0秒 |
 如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求:
如图,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经过3.0s落到斜坡上的A点.已知O点是斜坡的起点,斜坡与水平面的夹角θ=37°,运动员的质量m=50kg.不计空气阻力.(取sin37°=0.60,cos37°=0.80;g取10m/s2)求: