题目内容
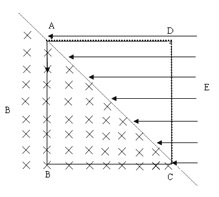
【题目】如图所示，一内壁粗糙的环形细圆管，位于竖直平面内，环的半径为R（比细管的直径大得多），在圆管中有一个直径与细管内径相同的小球（可视为质点），小球的质量为m，设某一时刻小球通过轨道的最低点时对管壁的压力为6mg。此后小球便作圆周运动，经过半个圆周恰能通过最高点，则在此过程中小球克服摩擦力所做的功是（ ）
A. 3mgR B. 2mgR C. mgR D. mgR/2
【答案】D
【解析】试题分析：根据牛顿第二定律求出小球通过最低点时的速度，因为小球恰能通过最高点，知最高点的速度为零，根据动能定理求出此过程中小球克服摩擦力所做的功．
根据牛顿第二定律得，在最低点有： 
，解得
．小球恰好经过最高点，则最高点的速度为0．根据动能定理得
，解得
，故D正确．
第1卷单元月考期中期末系列答案
【题目】某同学在做“研究匀变速直线运动”实验中，
(1)实验用的电火花打点计时器使用是电压是_____V的交流电源。已知打点计时器电源频率为50 Hz，则打相邻两点的时间间隔为 。
(2)请按照实验进行的先后顺序，将下述步骤的代号填在横线上 。
A．把穿过打点计时器的纸带固定在小车后面 |
B．把打点计时器固定在木板的没有滑轮的一端，连好电路，使有滑轮的一端伸出桌面 |
C．换上新的纸带再重做两次 |
D．使小车停在靠近打点计时器处，接通电源，放开小车，让小车运动 |
E．把一条细绳拴在小车上，细绳跨过定滑轮，下边吊着合适的钩码
F．断开电源，取出纸带
(3)如图所示，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带每两个相邻计数点间有四个点没有画出，其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm，则A点处瞬时速度的大小是 m/s，小车运动的加速度计算表达式为 ，加速度的大小是 m/s2。
