题目内容
【题目】如图，以O点为圆心、半径为R的圆形区域内有垂直于纸面向内的匀强磁场，磁感应强度大小为B，线段
是圆的一条直径，有一个质量为m、电荷量为+q的离子在纸面内从P点射入磁场，射入磁场时速度方向与
的夹角为30°．重力不计．
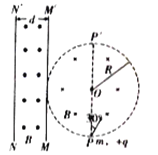
(1)若离子在
点离开圆形磁场区域，求离子的速度大小v0；
(2)现有大量该种离子，速率大小都是
，在纸面内沿各个方向通过P点进入圆形磁场区域，试通过计算找出离子只能在圆周的哪一部分射出圆形区域（不计离子间相互作用）；
(3)若在圆形区域左侧还存在一个以
、
为边界的条形区域磁场，磁感应强度大小与圆形区域内相同，两边界间距
，且有
，其中
与圆形区域相切．研究(2)问中离子的运动，求“射出圆形区域时的位置”与P点相距最远的那些离子，它们从P点进入圆形区域直到离开条形区域所用的时间．
【答案】（1）
（2）在P左侧磁场圆1/6个圆弧内 （3）
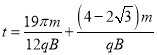
【解析】试题分析：（1）由几何关系得，离子在磁场中运动的轨迹半径r1=2R
由
，得
代入r1=2R解得： 
（2）将运动速度为
代入，可得离子在磁场中运动的轨迹半径为
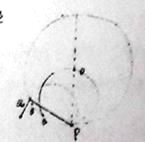
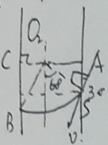
如图，Q为离子离开圆形区域位置，则根据几何性质， 
故令Q0为P点左侧圆形区域边界上一点，且PQ0=R，则磁场圆只能在Q0与P之间的一段劣弧上射出圆形区域， 
， 
，在P左侧，磁场圆上1/6个圆弧内
（3）如图，从Q0飞出圆形区域的离子即本问所说离子，在圆形区域中走过半圆，所以运动时间
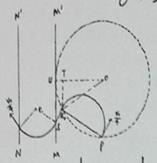
由几何关系得离子匀速直线运动路程
匀速运动时间为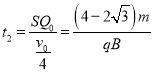
由几何关系得离子在条形磁场中： 
， 
可得
则转过的圆心角为
时间
总时间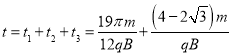
练习册系列答案
相关题目
