题目内容
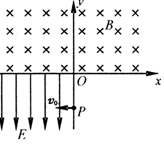
(08年黄冈市期末)(15分)如图所示,两根平行金属导轨MN、PQ相距为d=1.0m,导轨平面与水平面夹角为α=30°,导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计.整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中.金属棒ef垂直于MN、PQ静止放置,且与导轨保持良好接触,其长刚好为d、质量m=0.1kg、电阻r=0.4Ω,距导轨底端S1=3.75m.另一根与金属棒平行放置的绝缘棒gh长度也为d,质量为![]() ,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑S2=0.2m后再次静止,测得此过程中电阻R上产生的电热为Q=0.2J.已知两棒与导轨间的动摩擦因数均为
,从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰(碰撞时间极短),碰后金属棒沿导轨上滑S2=0.2m后再次静止,测得此过程中电阻R上产生的电热为Q=0.2J.已知两棒与导轨间的动摩擦因数均为![]() ,g取10m/s2,求:
,g取10m/s2,求:

(1)碰后瞬间两棒的速度;
(2)碰后瞬间的金属棒加速度;
(3)金属棒在导轨上运动的时间。
解析:(1)设金属棒碰后的速度为v,对金属棒碰后的过程运用动能定理:
0-![]() mv2=-W安-mgS2sinα-μmgS2cosα ①
mv2=-W安-mgS2sinα-μmgS2cosα ①
由功能关系,安培力做的功W安等于回路中总电热
![]() ②
②
设绝缘棒与金属棒碰前的速度为v1,对绝缘棒在导轨上滑动过程运用动能定理:
![]() ③
③
设绝缘棒碰后的速度为v2,两棒碰时满足动量守恒,选沿导轨向上的方向为正方向,有:
![]() ④
④
由①②得v=3m/s ⑤
由③④⑤得v2=-1m/s 负号表示方向沿导轨向下 ⑥
(2)切割磁感线产生的感应电动势为E,
E=Bdv ⑦
回路中的感应电流![]() ⑧
⑧
安培力的大小F安=BId ⑨
设金属棒的加速度为a,对金属棒运用牛顿第二定律:
μmgcosα+mgsinα+F安=ma ⑩
由⑦⑧⑨⑩式得:a=25m/s2,方向沿导轨平面向下 (11)
(3)设金属棒在导轨上运动时间为t,在此运动过程中,安培力的冲量为I安,沿导轨方向运用动量定理:
-I安-μmgtcosα-mgtsinα=0-mv (12)
其中I安=![]() ?△t (13)
?△t (13)
由闭合电路欧姆定律:![]() (14)
(14)
由法拉第电磁感应定律![]() (15)
(15)
联立⑩(11)(12)(13)得:t=0.2s (16)

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案(08年黄冈市期末)(12分)实验室有如下器材:
仪器 | 数量和规格 |
定值电阻R0 | 一只:阻值为20Ω左右 |
滑动变阻器R1 | 一只:总阻值40Ω |
小量程电流表A | 相同两块:量程100mA,内阻未知 |
电压表V | 相同两块:量程3V,内阻未知 |
直流电源 | 一个:电动势约为4V,内阻约为5Ω |
开关 | 一个:单刀单掷 |
导线 | 若干 |
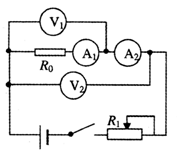
(1)为测量定值电阻的阻值和两表的内阻,某同学设计了如图10(甲)所示的电路.在某次测量中电压表![]() 的示数分别为1.20V、1.45V;电流表
的示数分别为1.20V、1.45V;电流表![]() 的示数分别为48.0mA、49.0mA,则定值电阻的阻值R0=___________Ω;电流表的内阻RA=___________Ω;电压表的内阻RV=___________Ω.(结果保留三位有效数字)
的示数分别为48.0mA、49.0mA,则定值电阻的阻值R0=___________Ω;电流表的内阻RA=___________Ω;电压表的内阻RV=___________Ω.(结果保留三位有效数字)

(2)为了进一步较精确测定电源的电动势和内阻,该同学从电表中选出一块电压表和一块电流表,结合其它器材,测出多组U和I的值,作出U―I图线,再由图线计算出电源的电动势和内阻。请设计出实验电路图,画在图乙中的方框内。