题目内容
如图所示,在x≥0的区域内存在与xOy平面垂直的匀强磁场,磁感应强度的大小为B,方向垂直于纸面向里。假设一束初速度为零的质量为m、带电荷量为q的正离子,经过加速电场加速后从O点沿x轴正方向进入匀强磁场区域。有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d)。正离子的重力不计。
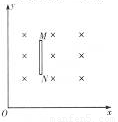
(1)加速电场的电压在什么范围内,进入磁场的离子才能全部打在金属板上?
(2)求打在金属板上的离子在磁场中运动的最短时间与最长时间的比值。(sin37°=0.6, cos37°=0.8)
(1)要使进入磁场的离子能全部打在金属板上,加速电压的取值范围应为
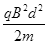 ≤
≤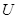 ≤
≤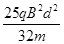
(2)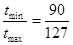
【解析】
试题分析:(1)设加速电压为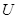 ,正离子初速度为零,经过加速电场加速,根据动能定理得
,正离子初速度为零,经过加速电场加速,根据动能定理得
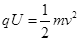 (1分)
(1分)
正离子在磁场中做匀速圆周运动,洛伦兹力提供向心力:
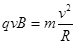 ,得
,得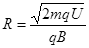 (2分)
(2分)

加速电压较小时,离子在磁场中做匀速圆周运动的半径较小,当离子恰好打到金属板下端点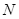 时,圆周运动的半径有最小值
时,圆周运动的半径有最小值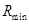 ,如图甲所示。
,如图甲所示。
根据几何知识可以判断: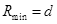 (1分)
(1分)
解得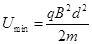 (2分)
(2分)
加速电压较大时,离子在磁场中做匀速圆周运动的半径较大,当离子恰好打到金属板上端点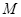 时,圆周运动的半径有最大值
时,圆周运动的半径有最大值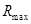 ,如图乙所示。
,如图乙所示。
根据几何知识可以判断: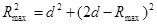 (1分)
(1分)
解得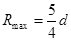 (1分)
(1分)
解得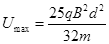 (2分)
(2分)
要使进入磁场的离子能全部打在金属板上,加速电压的取值范围应为
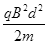 ≤
≤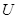 ≤
≤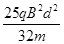 (1 分)
(1 分)
设离子在磁场中做匀速圆周运动的周期为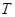 ,根据圆周运动规律得
,根据圆周运动规律得
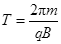 (2分)
(2分)
即离子在磁场中做匀速圆周运动的周期与加速电压无关。
打在金属板上的离子在图甲所示的轨迹中运动时间最短:
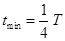 (1分)
(1分)
打在金属板上的离子在图乙所示的轨迹中运动时间最长:
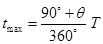 (1分)
(1分)
根据几何知识: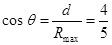 (1分)
(1分)
则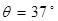
所以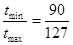 (2分)
(2分)
考点:洛伦兹力 匀速圆周运动


 如图所示,在x≤0的区域内存在匀强磁场B.矩形线框从t=0时刻起由静止开始沿x轴正向做匀加速直线运动,则线框中的感应电流I随时间t的变化图线是(设顺时针方向的电流为正)( )
如图所示,在x≤0的区域内存在匀强磁场B.矩形线框从t=0时刻起由静止开始沿x轴正向做匀加速直线运动,则线框中的感应电流I随时间t的变化图线是(设顺时针方向的电流为正)( ) (2005?丰台区一模)如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于xy平面(纸面)向里.具有一定电阻的矩形线框abcd位于xy平面内,线框的ab边与y轴重合.令线框从t=0的时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线I-t图可能是下图中的哪一个?( )
(2005?丰台区一模)如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于xy平面(纸面)向里.具有一定电阻的矩形线框abcd位于xy平面内,线框的ab边与y轴重合.令线框从t=0的时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线I-t图可能是下图中的哪一个?( )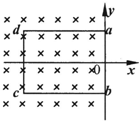 如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于纸面向里.矩形线框abcd从t=0时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线是( )
如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于纸面向里.矩形线框abcd从t=0时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线是( ) 如图所示,在x≥0的区域内存在垂直于xOy平面向里的匀强磁场,磁感应强度的大小为B.假设一系列速度不同,质量为m、电荷量为q的正离子从O点沿Ox轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d),不计离子的重力.具有下列速度的粒子能打在金属板上的是( )
如图所示,在x≥0的区域内存在垂直于xOy平面向里的匀强磁场,磁感应强度的大小为B.假设一系列速度不同,质量为m、电荷量为q的正离子从O点沿Ox轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d),不计离子的重力.具有下列速度的粒子能打在金属板上的是( )