题目内容
 如图所示,在x≥0的区域内存在垂直于xOy平面向里的匀强磁场,磁感应强度的大小为B.假设一系列速度不同,质量为m、电荷量为q的正离子从O点沿Ox轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d),不计离子的重力.具有下列速度的粒子能打在金属板上的是( )
如图所示,在x≥0的区域内存在垂直于xOy平面向里的匀强磁场,磁感应强度的大小为B.假设一系列速度不同,质量为m、电荷量为q的正离子从O点沿Ox轴正方向进入匀强磁场区域.有一块厚度不计、高度为d的金属板竖直放置在磁场中,截面如图,M、N分别为金属板截面的上、下端点,M点的坐标为(d,2d),N点的坐标为(d,d),不计离子的重力.具有下列速度的粒子能打在金属板上的是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:作出粒子运动轨迹的临界状态,结合几何关系求出恰好打到N点时的半径,再求出恰好打到M点的半径,根据洛伦兹力提供向心力求出粒子速度的范围.
解答:解:当离子恰好打到金属板下端点N点时,圆周运动的半径最小为Rmin,如图1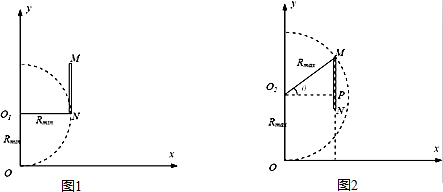
根据几何知识可以判断Rmin=d
当离子恰好打到金属板上端点M点时,圆周运动的半径最大为Rmax,如图2
根据几何知识判断:Rmax2=d2+(2d-Rmin)2
解得Rmax=
d.
根据qvB=m
得,v1=
,v2=
.
则粒子的速度
≤v≤
,可以打在金属板上.故C、D正确,A、B错误.
故选:CD.

根据几何知识可以判断Rmin=d
当离子恰好打到金属板上端点M点时,圆周运动的半径最大为Rmax,如图2
根据几何知识判断:Rmax2=d2+(2d-Rmin)2
解得Rmax=
| 5 |
| 4 |
根据qvB=m
| v2 |
| r |
| qBd |
| m |
| 5qBd |
| 4m |
则粒子的速度
| qBd |
| m |
| 5qBd |
| 4m |
故选:CD.
点评:此题考查离子在匀强磁场中的运动情况,属于高考常见题目,关键要抓住临界状态,结合牛顿第二定律进行求解.

练习册系列答案
相关题目

 如图所示,在x≤0的区域内存在匀强磁场B.矩形线框从t=0时刻起由静止开始沿x轴正向做匀加速直线运动,则线框中的感应电流I随时间t的变化图线是(设顺时针方向的电流为正)( )
如图所示,在x≤0的区域内存在匀强磁场B.矩形线框从t=0时刻起由静止开始沿x轴正向做匀加速直线运动,则线框中的感应电流I随时间t的变化图线是(设顺时针方向的电流为正)( ) (2005?丰台区一模)如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于xy平面(纸面)向里.具有一定电阻的矩形线框abcd位于xy平面内,线框的ab边与y轴重合.令线框从t=0的时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线I-t图可能是下图中的哪一个?( )
(2005?丰台区一模)如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于xy平面(纸面)向里.具有一定电阻的矩形线框abcd位于xy平面内,线框的ab边与y轴重合.令线框从t=0的时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线I-t图可能是下图中的哪一个?( )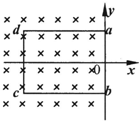 如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于纸面向里.矩形线框abcd从t=0时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线是( )
如图所示,在x≤0的区域内存在匀强磁场,磁场的方向垂直于纸面向里.矩形线框abcd从t=0时刻起由静止开始沿x轴正方向做匀加速运动,则线框中的感应电流I(取逆时针方向的电流为正)随时间t的变化图线是( )