题目内容
10.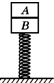 A、B两木块叠放在竖直轻弹簧上,如图所示.已知木块A、B质量分别为M=0.42kg和m=0.40kg,弹簧的劲度系数k=100N/m.若A、B静止在弹簧上,在木块A上作用一个竖直向上的力F,使A由静止开始竖直向上作匀加速直线运动经过0.4s木块A、B分离,使木块A竖直作匀加速运动的过程中.求:
A、B两木块叠放在竖直轻弹簧上,如图所示.已知木块A、B质量分别为M=0.42kg和m=0.40kg,弹簧的劲度系数k=100N/m.若A、B静止在弹簧上,在木块A上作用一个竖直向上的力F,使A由静止开始竖直向上作匀加速直线运动经过0.4s木块A、B分离,使木块A竖直作匀加速运动的过程中.求:(1)加速度;
(2)在分离前F做的功(g取10m/s2)
分析 (1)当A、B两物体的弹力N≠0时,木块A、B加速度相同,当N=0时,二者分离,由胡克定律求出初始状态和当N=0时,弹簧的压缩量,从而求出两物体上升的高度;然后结合牛顿第二定律、运动学的公式即可求出加速度的大小.
(2)根据据匀变速直线运动的公式求出AB的速度,对A、B组成的系统运用功能关系,即F所做的功等于系统动能的增量、重力势能的增量和弹性势能的减小量之和.
解答 解:(1)此题难点在于能否确定两物体分离的临界点.当F=0(即不加竖直向上F力)时,
设木块A、B叠放在弹簧上处于平衡时弹簧的压缩量为x,
有:kx=(mA+mB)g,即x=$\frac{({m}_{A}+{m}_{B})g}{k}$ ①
对木块A施加力F,A、B受力如图所示,对木块A有:F+N-mAg=mAa 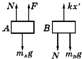 ②
②
对木块B有:kx-N-mBg=mBa ③
可知,当N≠0时,木块A、B加速度相同,由②式知欲使木块A匀加速运动,随N减小F增大;
当N=0时,A、B开始分离,由③式知,弹簧压缩量kx′=mB(a+g),则$x′=\frac{{m}_{B}(a+g)}{k}$④
向上运动的过程中:$x-x′=\frac{1}{2}a{t}^{2}$ ⑤
联立以上各式得:a=0.5m/s2
(2)木块A、B的共同速度:v2=2a(x-x′) ⑥
由题知,此过程弹性势能减少了:$△{E}_{P}=\frac{1}{2}k{x}^{2}-\frac{1}{2}kx{′}^{2}$ ⑦
设F力所做的功为WF,对这一过程应用功能原理,得:${W}_{F}=\frac{1}{2}({m}_{A}+{m}_{B}){v}^{2}+({m}_{A}+{m}_{B})g(x-x′)-△{E}_{P}$
联立①④⑤⑥式,得:${W}_{F}=9.64×1{0}^{-2}J$
答:(1)使木块A竖直做匀加速运动的过程中的加速度是0.5m/s2.
(2)这一过程F对木块做的功为9.64×10-2J.
点评 本题的过程较复杂,关键是理清过程,正确地受力分析,运用牛顿第二定律和功能关系进行求解.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案| A. | 只有很小的物体才能视为质点,很大的物体不能视为质点 | |
| B. | 做直线运动的物体,其位移大小跟这段时间内它通过的路程一定相等 | |
| C. | 若以河岸为参考系,在顺水漂流的船上行走的人可能是静止的 | |
| D. | 一节课45分钟,45分钟指的是下课的时刻 |
| A. | 电荷量很小的点电荷称元电荷 | |
| B. | 一个带电体的电荷量可以为元电荷的205.5倍 | |
| C. | 元电荷是最小的电荷量 | |
| D. | 元电荷没有正、负之分 |

| A. | a和b | B. | b和d | C. | a和d | D. | c和d |
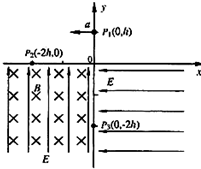 如图所示的坐标系中,x轴水平,y轴竖直,x轴上方空间只存在重力场,第Ⅲ象限存在沿y轴正方向的匀强电场和垂直xy平面向里的匀强磁场,在第Ⅳ象限有沿x轴负方向的匀强电场,场强与第Ⅲ象限存在的电场的场强大小相等.一质量为m,带电量为q的小球a,从轴上点P1(0,h)以一定的水平速度沿轴负方向抛出,它经过点P2(-2h,0)进入第Ⅲ象限,恰好做匀速圆周运动,又经过y轴上的点P3 (0,-2h)进入第Ⅳ象限,试求:
如图所示的坐标系中,x轴水平,y轴竖直,x轴上方空间只存在重力场,第Ⅲ象限存在沿y轴正方向的匀强电场和垂直xy平面向里的匀强磁场,在第Ⅳ象限有沿x轴负方向的匀强电场,场强与第Ⅲ象限存在的电场的场强大小相等.一质量为m,带电量为q的小球a,从轴上点P1(0,h)以一定的水平速度沿轴负方向抛出,它经过点P2(-2h,0)进入第Ⅲ象限,恰好做匀速圆周运动,又经过y轴上的点P3 (0,-2h)进入第Ⅳ象限,试求:
 如图所示,一修路工在长s=100m的隧道中的某位置A,突然发现一列火车出现在右隧道口外侧该隧道口200m处,修路工立即以大小为v1=4m/s的速度向左隧道口跑并恰好能脱离危险,已知火车的速度大小v2=20m/s,求位置A离右隧道口的距离.
如图所示,一修路工在长s=100m的隧道中的某位置A,突然发现一列火车出现在右隧道口外侧该隧道口200m处,修路工立即以大小为v1=4m/s的速度向左隧道口跑并恰好能脱离危险,已知火车的速度大小v2=20m/s,求位置A离右隧道口的距离.