题目内容
2. 如图所示,一修路工在长s=100m的隧道中的某位置A,突然发现一列火车出现在右隧道口外侧该隧道口200m处,修路工立即以大小为v1=4m/s的速度向左隧道口跑并恰好能脱离危险,已知火车的速度大小v2=20m/s,求位置A离右隧道口的距离.
如图所示,一修路工在长s=100m的隧道中的某位置A,突然发现一列火车出现在右隧道口外侧该隧道口200m处,修路工立即以大小为v1=4m/s的速度向左隧道口跑并恰好能脱离危险,已知火车的速度大小v2=20m/s,求位置A离右隧道口的距离.
分析 令位置A离右隧道口的距离为x,则汽车到达隧道左侧的时间小于工作到达隧道左侧的时间,由位移和速度关系求解即可.
解答 解:令位置A离右隧道口的距离为x,则工人奔跑的距离L=s-x,则由题意知:
$\frac{s+200}{{v}_{2}}=\frac{L}{{v}_{1}}$
即:$\frac{100+200}{20}=\frac{100-x}{4}$
解得:x=40m
答:位置A离右隧道口的距离为40m.
点评 解决此类问题是画出运动示意图,再注意它们在运动时间上具有等时性,然后根据位移找准相遇时的关系式.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.下面的带点物体中可以看成质点的是( )
| A. | 研究陀螺旋转时的陀螺 | |
| B. | 研究子弹穿过一张薄纸张的时间 | |
| C. | 研究地球自转运动时的地球 | |
| D. | 研究地球绕太阳公转运动时公转轨迹的地球 |
20. 某正点电荷的电场线分布如图所示,图中实线为电场线,虚线为等势面,则下列相关表述中正确的是( )
某正点电荷的电场线分布如图所示,图中实线为电场线,虚线为等势面,则下列相关表述中正确的是( )
 某正点电荷的电场线分布如图所示,图中实线为电场线,虚线为等势面,则下列相关表述中正确的是( )
某正点电荷的电场线分布如图所示,图中实线为电场线,虚线为等势面,则下列相关表述中正确的是( )| A. | M点和N点电场强度的大小相等 | |
| B. | M点和N点电场强度的方向相同 | |
| C. | M点和R点电势相同 | |
| D. | 根椐点电荷场强公式E=$\frac{kQ}{{r}^{2}}$,当r趋近于零时,场强E将无穷大 |
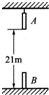 如图所示,A、B两棒各长1m,A吊于高处,B竖直置于地面上,A的下端距地面21m.现让两棒同时开始运动,A自由下落,B以20m/s的初速度竖直上抛,若不计空气阻力,求:
如图所示,A、B两棒各长1m,A吊于高处,B竖直置于地面上,A的下端距地面21m.现让两棒同时开始运动,A自由下落,B以20m/s的初速度竖直上抛,若不计空气阻力,求: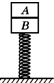 A、B两木块叠放在竖直轻弹簧上,如图所示.已知木块A、B质量分别为M=0.42kg和m=0.40kg,弹簧的劲度系数k=100N/m.若A、B静止在弹簧上,在木块A上作用一个竖直向上的力F,使A由静止开始竖直向上作匀加速直线运动经过0.4s木块A、B分离,使木块A竖直作匀加速运动的过程中.求:
A、B两木块叠放在竖直轻弹簧上,如图所示.已知木块A、B质量分别为M=0.42kg和m=0.40kg,弹簧的劲度系数k=100N/m.若A、B静止在弹簧上,在木块A上作用一个竖直向上的力F,使A由静止开始竖直向上作匀加速直线运动经过0.4s木块A、B分离,使木块A竖直作匀加速运动的过程中.求:
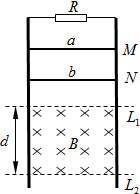 如图所示,电阻忽略不计的、两根平行的光滑金属导轨竖直放置,其上端接一阻值为3Ω的定值电阻R.在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B,磁场区域的高度为d=0.5m.导体棒a的质量ma=0.2kg、电阻Ra=3Ω;导体棒b的质量mb=0.1kg、电阻Rb=6Ω,它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当b 刚穿出磁场时a正好进入磁场.设重力加速度为g=10m/s2.(不计a、b之间的作用)求:
如图所示,电阻忽略不计的、两根平行的光滑金属导轨竖直放置,其上端接一阻值为3Ω的定值电阻R.在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B,磁场区域的高度为d=0.5m.导体棒a的质量ma=0.2kg、电阻Ra=3Ω;导体棒b的质量mb=0.1kg、电阻Rb=6Ω,它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当b 刚穿出磁场时a正好进入磁场.设重力加速度为g=10m/s2.(不计a、b之间的作用)求: