题目内容
如图所示,倾斜挡板NM上有一个小孔K,NM与水平挡板NP成60°角,K与N间的距离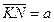 。现有质量为m,电荷量为q的正电粒子组成的粒子束,垂直于倾斜挡板NM,以速度v0不断射入,不计粒子所受的重力。
。现有质量为m,电荷量为q的正电粒子组成的粒子束,垂直于倾斜挡板NM,以速度v0不断射入,不计粒子所受的重力。

(1)若在NM和NP两档板所夹的区域内存在一个垂直于纸面向外的匀强磁场,NM和NP为磁场边界。粒子恰能垂直打在水平挡板NP上,求匀强磁场的磁感应强度的大小。
(2)若在NM和NP两档板所夹的区域内,只在某一部分区域存在一与(1)中大小相等方向相反的匀强磁场。从小孔K飞入的这些粒子经过磁场偏转后也能垂直打到水平挡板NP上(之前与挡板没有碰撞),求粒子在该磁场中运动的时间。
(3)若在(2)问中,磁感应强度大小未知,从小孔K飞入的这些粒子经过磁场偏转后能垂直打到水平挡板NP上(之前与挡板没有碰撞),求该磁场的磁感应强度的最小值。
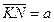 。现有质量为m,电荷量为q的正电粒子组成的粒子束,垂直于倾斜挡板NM,以速度v0不断射入,不计粒子所受的重力。
。现有质量为m,电荷量为q的正电粒子组成的粒子束,垂直于倾斜挡板NM,以速度v0不断射入,不计粒子所受的重力。 
(1)若在NM和NP两档板所夹的区域内存在一个垂直于纸面向外的匀强磁场,NM和NP为磁场边界。粒子恰能垂直打在水平挡板NP上,求匀强磁场的磁感应强度的大小。
(2)若在NM和NP两档板所夹的区域内,只在某一部分区域存在一与(1)中大小相等方向相反的匀强磁场。从小孔K飞入的这些粒子经过磁场偏转后也能垂直打到水平挡板NP上(之前与挡板没有碰撞),求粒子在该磁场中运动的时间。
(3)若在(2)问中,磁感应强度大小未知,从小孔K飞入的这些粒子经过磁场偏转后能垂直打到水平挡板NP上(之前与挡板没有碰撞),求该磁场的磁感应强度的最小值。
(1)粒子在磁场中作圆弧运动,由运动轨迹得: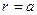
而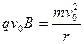 所以
所以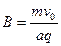
(2)如图所示,粒子垂直MN板从K点入射后做匀速直线运动从D点开始进入磁场,进入磁场后,根据左手定则,所受的洛伦兹力斜向上,要使粒子能垂直打到水平挡板NP,则粒子需偏转3000后从E射出(倾斜虚线可视为磁场的直线边界),做匀速直线运动垂直打到NP。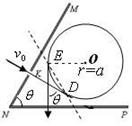
粒子在磁场中运动的周期为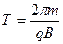
而
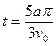
(3)要使B最小,则要半径r最大,临界情况是粒子圆周运动的轨迹恰好跟两挡板相切,如图所示。根据对称性圆周运动的圆心C、交点G位于∠MNP的角平分线上,则由几何关系可得:
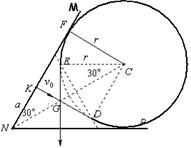
CDKF是边长为r的正方形。则在三角形NCF中,有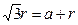 可得
可得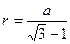
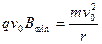
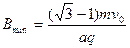
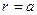
而
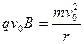 所以
所以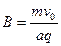
(2)如图所示,粒子垂直MN板从K点入射后做匀速直线运动从D点开始进入磁场,进入磁场后,根据左手定则,所受的洛伦兹力斜向上,要使粒子能垂直打到水平挡板NP,则粒子需偏转3000后从E射出(倾斜虚线可视为磁场的直线边界),做匀速直线运动垂直打到NP。

粒子在磁场中运动的周期为
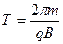
而

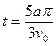
(3)要使B最小,则要半径r最大,临界情况是粒子圆周运动的轨迹恰好跟两挡板相切,如图所示。根据对称性圆周运动的圆心C、交点G位于∠MNP的角平分线上,则由几何关系可得:

CDKF是边长为r的正方形。则在三角形NCF中,有
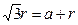 可得
可得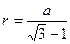
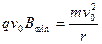
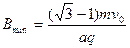
略

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目

 ,磁场的
,磁场的 边界平行于平行板A和B。
边界平行于平行板A和B。
 、质量为
、质量为 的带电粒子(重力不计),恰能从图中O点射出,且
的带电粒子(重力不计),恰能从图中O点射出,且 ,则A、B两板间的电压
,则A、B两板间的电压 是多少?
是多少?

 ,求离子乙的质量。
,求离子乙的质量。 的负离子,以速度v垂直磁感应强度为B的匀强磁场由.P点进入,界面I和Ⅱ平行,宽度为L(L<
的负离子,以速度v垂直磁感应强度为B的匀强磁场由.P点进入,界面I和Ⅱ平行,宽度为L(L< )要使离子由界面II飞出可改变离子的入射方向,离子所受重力不计,求离子在磁场中运动时间的最小值和最大值
)要使离子由界面II飞出可改变离子的入射方向,离子所受重力不计,求离子在磁场中运动时间的最小值和最大值

 (镭),
(镭),
