Question

【题目】如图所示，在游乐节目中，一质量为m＝60kg的选手以v0＝7m/s的水平速度抓住竖直绳下端的抓手开始摆动，当绳摆到与竖直方向夹角θ＝37°时，选手放开抓手，松手后的上升过程中选手水平速度保持不变，运动到水平传送带左端A时速度刚好水平，并在传送带上滑行，传送带以v＝2m/s匀速向右运动．已知绳子的悬挂点到抓手的距离为L＝6m，传送带两端点A、B间的距离s＝7m，选手与传送带的动摩擦因数为μ＝0．2，若把选手看成质点，且不考虑空气阻力和绳的质量．（g＝10m/s2，sin37°＝0．6，cos37°＝0．8）求：

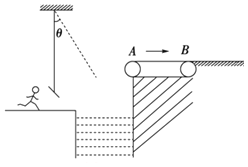
（1）选手放开抓手时的速度大小；

（2）选手在传送带上从A运动到B的时间

（3）选手在传送带上克服摩擦力做的功．

Answer 1

【答案】（1）5m/s （2）3s （3）360J

【解析】

试题分析：（1）设选手放开抓手时的速度为v1，则－mg（L－Lcosθ）＝mv12－mv02，v1＝5m/s

（2）设选手放开抓手时的水平速度为v2，v2＝v1cosθ①

选手在传送带上减速过程中 a＝－μg② v＝v2＋at1③ ④

匀速运动的时间t2，s－x1＝vt2⑤

选手在传送带上的运动时间t＝t1＋t2⑥

联立①②③④⑤⑥得：t＝3s

（3）由动能定理得Wf＝mv2－mv22，解得：Wf＝－360J

故克服摩擦力做功为360J．