题目内容

如图8所示，质量均为m的两物体A、B分别与轻质弹簧的两端相连接，将它们静止放在地面上.一质量也为m的小物体C从距A物体h高处由静止开始下落.C与A相碰后立即粘在一起向下运动，以后不再分开.当A与C运动到最高点时，物体B对地面刚好无压力.不计空气阻力.弹簧始终处于弹性限度内.已知重力加速度为g.求

图8

（1）A与C一起开始向下运动时的速度大小；

（2）A与C一起运动的最大加速度大小；

（3）弹簧的劲度系数.（提示：弹簧的弹性势能只由弹簧劲度系数和形变量大小决定）

解析：(1)设小物体C从静止开始运动到A点时速度为v,由机械能守恒定律mgh=mv2①,设C与A碰撞粘在一起时速度为v′,由动量守恒定律mv=(m+m)v′②,求出v′=③

(2)A与C一起将在竖直方向做简谐运动.当A与C运动到最高点时，回复力最大，加速度最大.A、C受力图，B受力图如图，B受力平衡有F=mg④,对A、C应用牛顿第二定律F+2mg=2ma⑤,求出a=1.5 g⑥,

图9

(3)设弹簧的劲度系数为k，开始时A

处于平衡状态，设弹簧的压缩形变量为Δx

对A有kΔx=mg⑦,当A与C运动到最高时，设弹簧的拉伸形变为

Δx′对B有kΔx′=mg⑧,由以上两式得Δx=Δx′⑨因此，在这两个位置时弹簧的弹性势能相等：E弹=E弹′⑩对A、C，从原平衡位置到最高点，根据机械能守恒定律E弹+（m+m）v′2=2mg(Δx+Δx′)+E弹′

解得k=.

答案：(1)  (2)1.5 g  (3)


练习册系列答案
相关题目

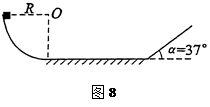
如图8所示，质量为m=0.2kg的小物体放在光滑的圆弧上端，圆弧半径R=55cm，下端接一长为1m的水平轨道AB，最后通过极小圆弧与倾角=37°的斜面相接，已知物体与水平面和斜面轨道的动摩擦因数均为0.1，将物体无初速度释放，求：

（1）物体第一次滑到水平轨道与右侧斜面轨道交接处的速度大小

（2）物体第一次滑上右侧斜轨道的最大高度（取g=10m/s2，cos37°=0.8，sin37°=0.6）

 
如图甲所示，质量均为m的、可视为质点的两个带电小球A，B被固定在弯成90°角的绝缘轻杆两端，OA和OB的长度均为L，可绕过O点的、与纸面垂直的水平轴无摩擦的转动，空气的作用力不计。已知A球带电量qA=+q，B球带电量qB=+3q，绝缘轻杆、A和B组成的系统在竖直向下的匀强电场中处于平衡状态，杆OA与竖直方向的夹角θ=53°，静电力常量用K表示，sin53°=0.8，cos53°=0.6。试求：
(1)竖直向下的匀强电场的场强E；
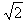(2)将带正电的、也可视为质点的小球C从无限远处缓慢地移入，使绝缘轻杆缓慢地转动，在小球C到轴O的正下方L处时。恰好使杆OA（与竖直方向的夹角θ=45°）处于平衡状态，如图乙所示，小球C带电量qC；
(3)在(2)的条件下，若已知小球C从无限远处缓慢地移到轴O的正下方L处的过程中，小球C克服匀强电场的电场力做功为W1，小球A，B，C之间的库仑力做功为W2，则在这个过程中匀强电场和小球A，B，C组成的整个系统的电势能变化量△W为多少？

 (2013·惠州模拟)如图8所示，质量分别为m1和m2的两物块放在水平地面上，与水平地面间的动摩擦因数都是μ(μ≠0)，且轻质弹簧将两物块连 接在一起，当用水平力F作用在m1上时，两物块均以加速度a做匀加速运动，此时，弹簧伸长量为x，若用水平力F′作用在m1上时，两物块均以加速度a′＝2a做匀加速运动，此时，弹簧伸长量为x′，则下列正确的是(　　)

A．F′＝2F                                          B．x′＝2x

C．F′>2F                                           D．x′<2x

 

图8

 

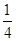如图8所示，质量为m=0.2kg的小物体放在光滑的圆弧上端，圆弧半径R=55cm，下端接一长为1m的水平轨道AB，最后通过极小圆弧与倾角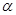=37°的斜面相接，已知物体与水平面和斜面轨道的动摩擦因数均为0.1，将物体无初速度释放，求：
（1）物体第一次滑到水平轨道与右侧斜面轨道交接处的速度大小
（2）物体第一次滑上右侧斜轨道的最大高度（取g=10m/s2，cos37°=0.8，sin37°=0.6）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网